题目内容
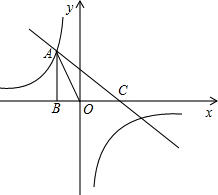 如图,已知反比例函数y1=
如图,已知反比例函数y1=| k |
| x |
| 3 |
| 3 |
(1)求k和m的值;
(2)若一次函数y2=ax+1的图象经过点A,并且与双曲线交于另一点C,求C的坐标,并直接写出x取何值时y1>y2.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据反比例函数系数的几何意义,利用△AOB的面积即可求出k值,然后把点A的坐标代入反比例函数解析式,计算即可得到m的值.
(2)把A的坐标代入y2=ax+1求得直线AC的解析式,然后联立方程组求得C的坐标,然后根据A、C的坐标结合图象即可求得x的取值.
(2)把A的坐标代入y2=ax+1求得直线AC的解析式,然后联立方程组求得C的坐标,然后根据A、C的坐标结合图象即可求得x的取值.
解答:解:∵△AOB的面积为
,
∴
|x|•|y|=
|k|=
,
解得|k|=2
,
∵反比例函数图象位于第二、四象限,
∴k<0,
∴k=-2
,
∴反比例函数解析式为y=-
,
∵反比例函数图象经过点A(-
,m),
∴-
=m,
解得m=2,
故k值为-2
,m值为2.
(2)∵一次函数y2=ax+1的图象经过点A(-
,2),
∴2=-
a+1,解得a=-
,
∴直线AC的解析式为y2=-
x+1,
解
得
或
,
∴C的坐标为(2
,-1),
根据A、C的坐标,根据图象可知:当x<-
或0<x<2
时y1>y2.
| 3 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
解得|k|=2
| 3 |
∵反比例函数图象位于第二、四象限,
∴k<0,
∴k=-2
| 3 |
∴反比例函数解析式为y=-
2
| ||
| x |
∵反比例函数图象经过点A(-
| 3 |
∴-
2
| ||
-
|
解得m=2,
故k值为-2
| 3 |
(2)∵一次函数y2=ax+1的图象经过点A(-
| 3 |
∴2=-
| 3 |
| ||
| 3 |
∴直线AC的解析式为y2=-
| ||
| 3 |
解
|
|
|
∴C的坐标为(2
| 3 |
根据A、C的坐标,根据图象可知:当x<-
| 3 |
| 3 |
点评:本题考查了反比例函数和一次函数图象的交点问题,反比例函数系数的几何意义,反比例函数图象上点的坐标特征,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,三角形的面积是
|k|.
| 1 |
| 2 |

练习册系列答案
相关题目
 如图,⊙01和⊙O2外切,AB是外公切线,延长O1O2交AB的延长线于C点,若∠C=30°,AB=2,求两圆的半径.
如图,⊙01和⊙O2外切,AB是外公切线,延长O1O2交AB的延长线于C点,若∠C=30°,AB=2,求两圆的半径.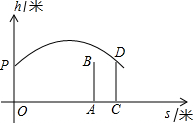 甲、乙两人进行羽毛球比赛,甲发出一颗十分关键的球,出手点为P,羽毛球飞出的水平距离s(米)与其距地面高度h(米)之间的关系式为h=-s2+5s+8.如图,球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为2米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是
甲、乙两人进行羽毛球比赛,甲发出一颗十分关键的球,出手点为P,羽毛球飞出的水平距离s(米)与其距地面高度h(米)之间的关系式为h=-s2+5s+8.如图,球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为2米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是 如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点,连接BE交AD于点F,且BF=AC,过点D作DG∥AB交AC于点G.
如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点,连接BE交AD于点F,且BF=AC,过点D作DG∥AB交AC于点G.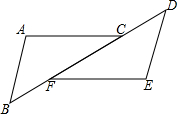 如图∠A=∠E,AB∥DE,BF=CD,说明AC与EF的关系.
如图∠A=∠E,AB∥DE,BF=CD,说明AC与EF的关系. 已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.求sinA的值.
已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.求sinA的值.