题目内容
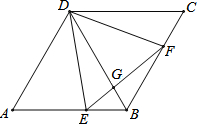 如图,在菱形ABCD中,∠A=60°,点E、F分别在边AB、BC上,EF与BD交于G,且∠DEF=60°.
如图,在菱形ABCD中,∠A=60°,点E、F分别在边AB、BC上,EF与BD交于G,且∠DEF=60°.(1)求证:△ADE∽△BEG;
(2)已知AD=3,AE=2,求sin∠BEF的值(结果保留根号).
考点:相似三角形的判定与性质,菱形的性质
专题:
分析:(1)由菱形ABCD,∠A=60°,得出∠ABC=120°,再由BD平分∠ABC,得出∠EBG=60°=∠A,由∠DEB=∠A+∠ADE,得出∠ADE=∠BEG,证出△ADE∽△BEG;
(2)作EH⊥AD于H,由△ADE∽△BEG,得出∠BEF=∠ADE,求出sin∠ADE即可.
(2)作EH⊥AD于H,由△ADE∽△BEG,得出∠BEF=∠ADE,求出sin∠ADE即可.
解答:(1)证明:∵四边形ABCD是菱形,∠A=60°,
∴∠ABC=120°,BD平分∠ABC,
∴∠EBG=60°,
∵∠DEB=∠A+∠ADE,∠DEF=60°,
∴∠ADE=∠BEG,
∴△ADE∽△BEG;
(2)解:作EH⊥AD于H,如图所示: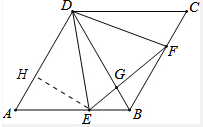
则∠AEH=90°-60°=30°,
∴AH=
AE=1,
∴EH=
,
∵AD=AB=2+1=3,
∴DH=2,
在Rt△DEH中,根据勾股定理得,DE=
=
,
由(1)得,∠BEF=∠ADE,
∴sin∠BEF=sin∠ADE=
=
.
∴∠ABC=120°,BD平分∠ABC,
∴∠EBG=60°,
∵∠DEB=∠A+∠ADE,∠DEF=60°,
∴∠ADE=∠BEG,
∴△ADE∽△BEG;
(2)解:作EH⊥AD于H,如图所示:

则∠AEH=90°-60°=30°,
∴AH=
| 1 |
| 2 |
∴EH=
| 3 |
∵AD=AB=2+1=3,
∴DH=2,
在Rt△DEH中,根据勾股定理得,DE=
22+(
|
| 7 |
由(1)得,∠BEF=∠ADE,
∴sin∠BEF=sin∠ADE=
| ||
|
| ||
| 7 |
点评:本题考查了菱形的性质和相似三角形的判定与性质以及锐角三角函数的运用,证明三角形相似是解决问题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 如图是一数值转换机,若输入的数为-
如图是一数值转换机,若输入的数为-| 1 |
| 2 |
| A、-6 | B、-3 | C、0 | D、3 |
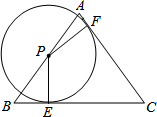 如图,△ABC中AB=AC=5,BC=6,点P在边AB上,以P为圆心的⊙P分别与边AC、BC相切于点E、F,则⊙P的半径PE的长为( )
如图,△ABC中AB=AC=5,BC=6,点P在边AB上,以P为圆心的⊙P分别与边AC、BC相切于点E、F,则⊙P的半径PE的长为( )A、
| ||
| B、2 | ||
C、
| ||
D、
|
 如图,平行四边形ABCD中,对角线AC、BD相交于点O,过点O作PF⊥BC于点F,交AD于点E,交BA的延长线于点P.若PE=EO=2,PA=3,则△OBC的面积等于
如图,平行四边形ABCD中,对角线AC、BD相交于点O,过点O作PF⊥BC于点F,交AD于点E,交BA的延长线于点P.若PE=EO=2,PA=3,则△OBC的面积等于 如图,⊙01和⊙O2外切,AB是外公切线,延长O1O2交AB的延长线于C点,若∠C=30°,AB=2,求两圆的半径.
如图,⊙01和⊙O2外切,AB是外公切线,延长O1O2交AB的延长线于C点,若∠C=30°,AB=2,求两圆的半径. 抛物线y=
抛物线y= 如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点,连接BE交AD于点F,且BF=AC,过点D作DG∥AB交AC于点G.
如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点,连接BE交AD于点F,且BF=AC,过点D作DG∥AB交AC于点G.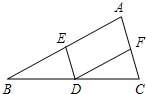 如图,在△ABC中,D点在BC边上,DE∥A C,DF∥AB.
如图,在△ABC中,D点在BC边上,DE∥A C,DF∥AB.