题目内容
12．计算：$\frac{{x}^{-2}-{y}^{-2}}{{x}^{-1}+{y}^{-1}}$+$\frac{1}{y}$-$\frac{1}{x}$．分析 根据分式运算的法则以及负整数指数幂的意义即可求出答案．
解答 解：原式=$\frac{\frac{1}{{x}^{2}}-\frac{1}{{y}^{2}}}{\frac{1}{x}-\frac{1}{y}}$+$\frac{1}{y}$-$\frac{1}{x}$
=$\frac{（\frac{1}{x}+\frac{1}{y}）（\frac{1}{x}-\frac{1}{y}）}{\frac{1}{x}+\frac{1}{y}}$+$\frac{1}{y}$-$\frac{1}{x}$
=$\frac{1}{x}$-$\frac{1}{y}$+$\frac{1}{y}$-$\frac{1}{x}$
=0
点评 本题考查学生的计算能力，涉及因式分解，分式约分与分式加减等知识，负整数指数幂的意义，属于中等题型
练习册系列答案
相关题目
“三月三，放风筝”如图是小东同学自己做的风筝，他根据AB=AD，BC=DC，不用度量，就知道∠ABC=∠ADC．请用所学的知识给予说明．
唐代大诗人李白喜好饮酒作诗，民间有“李白斗酒诗百篇”之说．《算法统宗》中记载了一个“李白沽酒”的故事．诗云：
1．下列运算正确的是（ ）
| A． | -a+b+c+d=-（a-b）-（-c-d） | B． | x-（y-z）=x-y-z | ||
| C． | x+2y-2z=x-2（z+y） | D． | -（x-y+z）=-x-y-z |
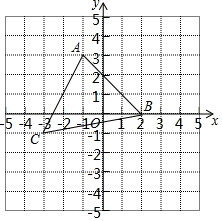如图，在平面直角坐标系中有一个△ABC，顶点A（-1，3），B（2，0），C（-3，-1）．