题目内容
在平面直角坐标系,己知点B(3,0),点C(0,-4),△ABC为等腰三角形,若点A在x轴上,则满足条件的点A有几个?表示它们的坐标.
考点:等腰三角形的判定,坐标与图形性质
专题:
分析:分为三种情况:①AB=BC,②AB=AC,③AC=BC,画出图形,即可得出答案.
解答:解答:解:∵点B(3,0),点C(0,-4),
∴OB=3.OC=4,
∴BC=5,
如图:

①以B为圆心,以BC为半径作弧,交x轴于A1、A2,此时A1、(8,0),A2,(-2,0);
②作BC的垂直平分线交x轴于A3,此时A3(-
,0);
③以C为圆心,以BC为半径作弧,交x轴于A4,此时A4(-3,0);
共2+1+1=4个点满足条件,
答:满足条件的点A有4个.
∴OB=3.OC=4,
∴BC=5,
如图:

①以B为圆心,以BC为半径作弧,交x轴于A1、A2,此时A1、(8,0),A2,(-2,0);
②作BC的垂直平分线交x轴于A3,此时A3(-
| 7 |
| 6 |
③以C为圆心,以BC为半径作弧,交x轴于A4,此时A4(-3,0);
共2+1+1=4个点满足条件,
答:满足条件的点A有4个.
点评:本题考查了等腰三角形的判定,坐标与图形性质的应用,用了分类讨论思想.

练习册系列答案
相关题目
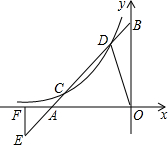 已知直线y=x+3与x轴、y轴分别交于A,B点,与y=
已知直线y=x+3与x轴、y轴分别交于A,B点,与y= 如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,求∠A、∠ACD、∠D之间的数量关系.
如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,求∠A、∠ACD、∠D之间的数量关系.