题目内容
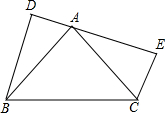 如图,在△ABC中,AB=AC,BD、CE垂直于过点A的直线,垂足分别为D、E,若AD=CE,问∠BAC=
如图,在△ABC中,AB=AC,BD、CE垂直于过点A的直线,垂足分别为D、E,若AD=CE,问∠BAC=考点:全等三角形的判定与性质
专题:
分析:求出∠BDA=∠CEA=90°,根据HL证Rt△BDA≌Rt△AEC,根据全等三角形的性质推出∠BAD=∠ACE,求出∠BAD+∠CAE=90°即可.
解答:解:∵BD、CE垂直于过点A的直线,垂足分别为D、E,
∴∠BDA=∠CEA=90°,
在Rt△BDA和Rt△AEC中
∴Rt△BDA≌Rt△AEC(HL),
∴∠BAD=∠ACE,
∵∠CEA=90°,
∴∠ACE+∠CAE=90°,
∴∠BAD+∠CAE=90°,
∴∠BAC=180°-90°=90°,
故答案为:90°.
∴∠BDA=∠CEA=90°,
在Rt△BDA和Rt△AEC中
|
∴Rt△BDA≌Rt△AEC(HL),
∴∠BAD=∠ACE,
∵∠CEA=90°,
∴∠ACE+∠CAE=90°,
∴∠BAD+∠CAE=90°,
∴∠BAC=180°-90°=90°,
故答案为:90°.
点评:本题考查了全等三角形的性质和判定,三角形内角和定理的应用,注意:全等是三角形的对应边相等,对应角相等.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
计算1-(-2)的结果为( )
| A、-1 | B、1 | C、3 | D、-3 |
 如图所示根据图中给出的零件的数据,求∠α的度数.
如图所示根据图中给出的零件的数据,求∠α的度数. 在长方形ABCD中,AD=8cm,AB=6cm,沿对角线BD把△BCD翻折至△BDE,如图.
在长方形ABCD中,AD=8cm,AB=6cm,沿对角线BD把△BCD翻折至△BDE,如图.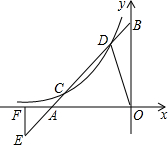 已知直线y=x+3与x轴、y轴分别交于A,B点,与y=
已知直线y=x+3与x轴、y轴分别交于A,B点,与y= 如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,求∠A、∠ACD、∠D之间的数量关系.
如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,求∠A、∠ACD、∠D之间的数量关系.