题目内容
2.用适当方法解方程(1)x2+6x-5=0
(2)3x(x-1)=2-2x.
分析 (1)先利用配方法得到(x+3)2=14,然后利用直接开平方法解方程;
(2)先移项得到3x(x-1)+2(x-1)=0,然后利用因式分解法解方程.
解答 解:(1)x2+6x=5,
x2+6x+9=14,
(x+3)2=14,
x+3=±$\sqrt{14}$,
所以x1=-3+$\sqrt{14}$,x2=-3-$\sqrt{14}$;
(2)3x(x-1)+2(x-1)=0,
(x-1)(3x+2)=0,
x-1=0或3x+2=0,
所以x1=1,x2=-$\frac{2}{3}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法解一元二次方程.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
12.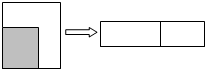 如图,边长为(m+2)的正方形纸片剪出一个边长为m的正方形之后余下部分又剪开拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为2,其面积是( )
如图,边长为(m+2)的正方形纸片剪出一个边长为m的正方形之后余下部分又剪开拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为2,其面积是( )
 如图,边长为(m+2)的正方形纸片剪出一个边长为m的正方形之后余下部分又剪开拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为2,其面积是( )
如图,边长为(m+2)的正方形纸片剪出一个边长为m的正方形之后余下部分又剪开拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为2,其面积是( )| A. | 2m+4 | B. | 4m+4 | C. | m+4 | D. | 2m+2 |
7.下列数中,是有理数的是( )
| A. | π | B. | (-2$\sqrt{3}$)2 | C. | $\sqrt{2}$ | D. | $\root{3}{9}$ |
12.某城市2011年底已有绿化面积300公顷,经过两年绿化,绿化面积逐年增加,到2013年底增加到363公顷.设绿化面积平均每年的增长率为x,由题意,所列方程正确的是( )
| A. | 300(1+x)=363 | B. | 300(1+x)2=363 | C. | 300(1+2x)=363 | D. | 363(1-x)2=300 |
 如图,点P是∠ABC内一点.
如图,点P是∠ABC内一点.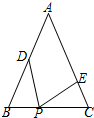 如图,△ABC中,AB=AC,∠A=50°,BP=CE,BD=CP,∠DPE的度数是65°.
如图,△ABC中,AB=AC,∠A=50°,BP=CE,BD=CP,∠DPE的度数是65°.