题目内容
12．
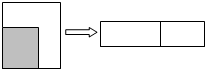如图，边长为（m+2）的正方形纸片剪出一个边长为m的正方形之后余下部分又剪开拼成一个长方形（不重叠无缝隙），若拼成的长方形一边长为2，其面积是（ ）| A． | 2m+4 | B． | 4m+4 | C． | m+4 | D． | 2m+2 |
分析 由于边长为（m+2）的正方形纸片剪出一个边长为m的正方形之后，剩余部分又剪拼成一个矩形（不重叠无缝隙），那么根据正方形的面积公式，可以求出剩余部分的面积，而矩形一边长为2，利用矩形的面积公式即可求出另一边长，即可求出去面积．
解答 解：依题意得剩余部分为
（m+2）2-m2=m2+4m+4-m2=4m+4，
而拼成的矩形一边长为2，
∴另一边长是（4m+4）÷2=2m+2．
∴面积为2（2m+2）=4m+4．
故选B．
点评 本题主要考查了多项式除以单项式，解题关键是熟悉除法法则．
练习册系列答案
相关题目
11．下列命题中的真命题是（ ）
| A． | 菱形是中心对称图形，但不是轴对称图形 | |
| B． | 相等的弦所对应的弦心距相等 | |
| C． | 直角三角形的外心和重心之间的距离等于斜边的六分之一 | |
| D． | 三角形的内心是三角形三边的中垂线的交点 |
20．25的平方根是（ ）
| A． | ±5 | B． | -5 | C． | 5 | D． | 25 |
17．
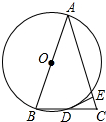如图，△ABC中，AB=AC，以边AB为直径作⊙O，交BC于点D，过D作DE⊥AC于点E．
（1）求证：DE为⊙O的切线；
（2）若AB=13，sinB=$\frac{12}{13}$，求CE的长．
如图，△ABC中，AB=AC，以边AB为直径作⊙O，交BC于点D，过D作DE⊥AC于点E．（1）求证：DE为⊙O的切线；
（2）若AB=13，sinB=$\frac{12}{13}$，求CE的长．
1．等腰直角三角形的斜边长为a，则其斜边上的高为（ ）
| A． | $\frac{a}{2}$ | B． | $\sqrt{2}a$ | C． | $\frac{\sqrt{3}}{2}$a | D． | $\frac{\sqrt{2}}{4}$a |