题目内容
15．
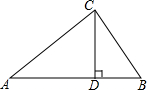如图，△ABC中，CD⊥AB于D，若AD=2BD，AC=6，BC=4，求BD的长．
分析 设BD=x，根据勾股定理列出方程，解方程即可．
解答 解：设BD=x，则AD=2x，
在Rt△ACD中，由勾股定理得，AC2-AD2=CD2，
在Rt△BCD中，BC2-BD2=CD2，
∴AC2-AD2=BC2-BD2，即62-（2x）2=42-x2，
解得，x=$\frac{2\sqrt{15}}{3}$，
则BD=$\frac{2\sqrt{15}}{3}$．
点评 本题考查的是勾股定理的应用，直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
5．
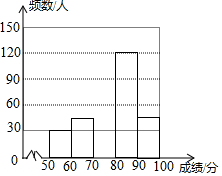为了弘扬苏州优秀传统文化，某中学举办了苏州文化知识大赛，其规则是：每位参赛选手回答100道选择题，答对一题得1分，不答或错答不得分、不扣分．赛后对全体参赛选手的成绩进行统计后，绘制了图中两幅不完整的答题情况的统计图．
根据图中信息，解答下列问题：
（1）a=0.15，b=60；
（2）补全频数分布直方图；
（3）若绘制“答题情况的扇形统计图”，求成绩在“90≤x＜100”组对应的扇形圆心角的度数．
为了弘扬苏州优秀传统文化，某中学举办了苏州文化知识大赛，其规则是：每位参赛选手回答100道选择题，答对一题得1分，不答或错答不得分、不扣分．赛后对全体参赛选手的成绩进行统计后，绘制了图中两幅不完整的答题情况的统计图． | 成绩分组 （x/分） | 频数（人） | 频率 |
| 50≤x＜60 | 30 | 0.10 |
| 60≤x＜70 | 45 | a |
| 70≤x＜80 | b | 0.20 |
| 80≤x＜90 | 120 | 0.40 |
| 90≤x＜100 | 45 | 0.15 |
（1）a=0.15，b=60；
（2）补全频数分布直方图；
（3）若绘制“答题情况的扇形统计图”，求成绩在“90≤x＜100”组对应的扇形圆心角的度数．
3．把两张同样的长方形纸卷成形状不同的圆柱形筒，并另装上两个底面，那么这两个圆柱的（ ）一定相等．
| A． | 表面积 | B． | 体积 | C． | 侧面积 |
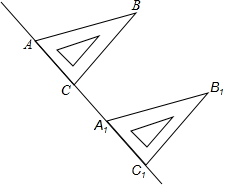如图，同学们用直尺和三角板画平行线，将一块三角板ABC的一边AC贴着直尺推移到A1B1C1的位置．
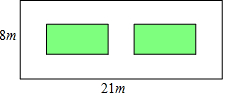某小区有一块长21米，宽8米的矩形空地，如图所示．社区计划在其中修建两块完全相同的矩形绿地，并且两块绿地之间及四周都留有宽度为x米的人行通道．如果这两块绿地的面积之和为60平方米，人行通道的宽度应是多少米？