题目内容
1.若函数$y=\frac{3}{x}$与y=x+1的图象交于点A(a,b),则$\frac{1}{a}-\frac{1}{b}$的值为( )| A. | $\frac{1}{3}$ | B. | 3 | C. | $-\frac{1}{3}$ | D. | -3 |
分析 先把A(a,b)分别代入两个解析式得到b=$\frac{3}{a}$,b=a-1,则ab=3,b-a=-1,再变形$\frac{1}{a}-\frac{1}{b}$得到$\frac{b-a}{ab}$,然后利用整体思想进行计算即可.
解答 解:把A(a,b)代入$y=\frac{3}{x}$与y=x+1得b=$\frac{3}{a}$,b=a-1,即ab=3,b-a=-1,
所以$\frac{1}{a}-\frac{1}{b}$=$\frac{b-a}{ab}$=-$\frac{1}{3}$.
故选:C.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数图象与一次函数图象的交点坐标满足两函数的解析式.

练习册系列答案
相关题目
6.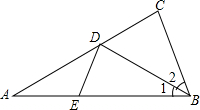 如图,在△ABC中,AB=AC,∠A=36°,∠1=∠2,∠ADE=$\frac{1}{2}$∠EDB,则∠DEB=( )
如图,在△ABC中,AB=AC,∠A=36°,∠1=∠2,∠ADE=$\frac{1}{2}$∠EDB,则∠DEB=( )
 如图,在△ABC中,AB=AC,∠A=36°,∠1=∠2,∠ADE=$\frac{1}{2}$∠EDB,则∠DEB=( )
如图,在△ABC中,AB=AC,∠A=36°,∠1=∠2,∠ADE=$\frac{1}{2}$∠EDB,则∠DEB=( )| A. | 36° | B. | 54° | C. | 60° | D. | 72° |
13.在一张1:100的地图上1cm2的面积的地,其实际面积是( )
| A. | 10000cm2 | B. | 1000cm2 | C. | 10cm2 | D. | 100cm2 |
 现有一块长40cm,宽20cm的长方形铁皮,在它的四个角分别剪去一个大小完全相同的小正方形,用剩余的部分做成一个底面积为300cm2的无盖长方体盒子,请求出剪去的小正方形的边长.
现有一块长40cm,宽20cm的长方形铁皮,在它的四个角分别剪去一个大小完全相同的小正方形,用剩余的部分做成一个底面积为300cm2的无盖长方体盒子,请求出剪去的小正方形的边长. 如图,已知:AD⊥BC,EF⊥BC,∠1=∠2.求证:
如图,已知:AD⊥BC,EF⊥BC,∠1=∠2.求证: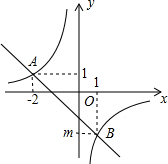 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A、B两点.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A、B两点.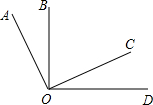 如图,∠AOC与∠BOD都是直角,若∠COD=30°,试求∠AOD,∠BOC的度数.
如图,∠AOC与∠BOD都是直角,若∠COD=30°,试求∠AOD,∠BOC的度数.