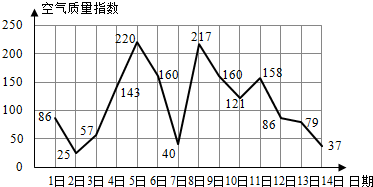
题目内容
11．计算：（$\frac{2x}{x+y}$-$\frac{x+2y}{x+y}$）÷$\frac{x-2y}{{x}^{2}-{y}^{2}}$．分析 原式括号中两项利用同分母分式的减法法则计算，同时利用除法法则变形，约分即可得到结果．
解答 解：原式=$\frac{2x-x-2y}{x+y}$•$\frac{（x+y）（x-y）}{x-2y}$=$\frac{x-2y}{x+y}$•$\frac{（x+y）（x-y）}{x-2y}$=x-y．
点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
1．若函数$y=\frac{3}{x}$与y=x+1的图象交于点A（a，b），则$\frac{1}{a}-\frac{1}{b}$的值为（ ）
| A． | $\frac{1}{3}$ | B． | 3 | C． | $-\frac{1}{3}$ | D． | -3 |
2．
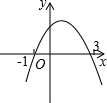如图，抛物线y=ax2+bx+c经过点（-1，0），与x轴的另一个交点在点（2，0）和点（3，0）之间，与y轴相交于正半轴：①b=a+c；②a+b＞0；③2a+b＞0；④$\frac{{b}^{2}-4ac}{4a}$+a+b+c＜0中，正确结论的个数是（ ）
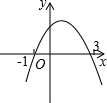如图，抛物线y=ax2+bx+c经过点（-1，0），与x轴的另一个交点在点（2，0）和点（3，0）之间，与y轴相交于正半轴：①b=a+c；②a+b＞0；③2a+b＞0；④$\frac{{b}^{2}-4ac}{4a}$+a+b+c＜0中，正确结论的个数是（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
如图，?ABCD的对角线AC、BD相交于点O，点E、F分别是线段AO、BO的中点，若EF=3，△OAB的周长是14，则AC+BD=16．
16．在下列实数：$\frac{1}{3}$，$\sqrt{2}$，-$\sqrt{3}$，π，3.14中任取一个，取到有理数的概率为（ ）
| A． | 0.2 | B． | 0.4 | C． | 0.6 | D． | 0.8 |
3．
已知y=ax2+bx+c的图象如图所示，则y=ax-bc的图象一定不经过（ ）
已知y=ax2+bx+c的图象如图所示，则y=ax-bc的图象一定不经过（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
