题目内容
12. 如图,已知:AD⊥BC,EF⊥BC,∠1=∠2.求证:
如图,已知:AD⊥BC,EF⊥BC,∠1=∠2.求证:(1)AB∥GD;
(2)∠3=∠B.
分析 (1)由条件可先证明AD∥EF,可求得∠1=∠EAD,结合条件可证明AB∥DG;
(2)根据“由垂直得直角”得到∠1+∠B=∠2+∠3=90°,结合(1)中的∠1=∠2,利用等量代换得到∠3=∠B.
解答  证明:(1)∵AD⊥BC,EF⊥BC,
证明:(1)∵AD⊥BC,EF⊥BC,
∴AD∥EF,
∴∠1=∠EAD.
∵∠1=∠2,
∴∠2=∠EAD,
∴AB∥GD;
(2)∵AD⊥BC,EF⊥BC,
∴∠1+∠B=∠2+∠3=90°,
∵由(1)知,∠1=∠2,
∴∠3=∠B.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
1.若函数$y=\frac{3}{x}$与y=x+1的图象交于点A(a,b),则$\frac{1}{a}-\frac{1}{b}$的值为( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | $-\frac{1}{3}$ | D. | -3 |
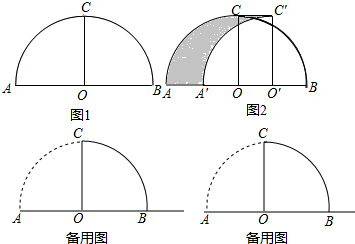
 如图,AC和BD相交于点O,且AB∥DC,OC=OD.求证:△OAB是等腰三角形.
如图,AC和BD相交于点O,且AB∥DC,OC=OD.求证:△OAB是等腰三角形.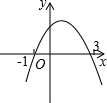 如图,抛物线y=ax2+bx+c经过点(-1,0),与x轴的另一个交点在点(2,0)和点(3,0)之间,与y轴相交于正半轴:①b=a+c;②a+b>0;③2a+b>0;④$\frac{{b}^{2}-4ac}{4a}$+a+b+c<0中,正确结论的个数是( )
如图,抛物线y=ax2+bx+c经过点(-1,0),与x轴的另一个交点在点(2,0)和点(3,0)之间,与y轴相交于正半轴:①b=a+c;②a+b>0;③2a+b>0;④$\frac{{b}^{2}-4ac}{4a}$+a+b+c<0中,正确结论的个数是( )