题目内容
6.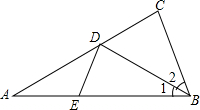 如图,在△ABC中,AB=AC,∠A=36°,∠1=∠2,∠ADE=$\frac{1}{2}$∠EDB,则∠DEB=( )
如图,在△ABC中,AB=AC,∠A=36°,∠1=∠2,∠ADE=$\frac{1}{2}$∠EDB,则∠DEB=( )| A. | 36° | B. | 54° | C. | 60° | D. | 72° |
分析 由等腰三角形的性质可求得∠1=∠2=∠A=36°,再结合条件可求得∠EDB,在△BDE中,由三角形内角和定理可求得∠DEB.
解答 解:∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°,
∴∠1=∠2,
∴∠1=∠2=36°,
∴∠ADB=180°-36°-36°=108°,
∵∠ADE=$\frac{1}{2}$∠EDB,
∴∠EDB=72°,
在△BDE中,∠DEB=180°-∠1-∠EDB=180°-36°-72°=72°,
故选D.
点评 本题主要考查等腰三角形的性质,利用等腰三角形的两底角相等的性质和已知条件求得∠EDB的度数是解题的关键.

练习册系列答案
相关题目
1.若函数$y=\frac{3}{x}$与y=x+1的图象交于点A(a,b),则$\frac{1}{a}-\frac{1}{b}$的值为( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | $-\frac{1}{3}$ | D. | -3 |
11.0.027的立方根是( )
| A. | 0.3 | B. | ±0.3 | C. | 0.03 | D. | ±0.03 |
16.在下列实数:$\frac{1}{3}$,$\sqrt{2}$,-$\sqrt{3}$,π,3.14中任取一个,取到有理数的概率为( )
| A. | 0.2 | B. | 0.4 | C. | 0.6 | D. | 0.8 |
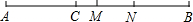 如图,线段AB的长为8cm,C是线段AB上的一点,AC=3.2cm,M是AB的中点,N是CB的中点.
如图,线段AB的长为8cm,C是线段AB上的一点,AC=3.2cm,M是AB的中点,N是CB的中点. 如图,将图案绕点O按逆时针方向旋转90°,得到的图案是( )
如图,将图案绕点O按逆时针方向旋转90°,得到的图案是( )



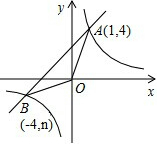 已知,如图,反比例函数$y=\frac{k}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)、B(-4,n),
已知,如图,反比例函数$y=\frac{k}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)、B(-4,n),