题目内容
8.计算:(1)($\sqrt{24}$-$\sqrt{\frac{1}{2}}$)-($\sqrt{\frac{1}{8}}$+$\sqrt{6}$)
(2)2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$÷$\sqrt{50}$.
分析 根据二次根式的混合运算法则计算即可.
解答 解:(1)($\sqrt{24}$-$\sqrt{\frac{1}{2}}$)-($\sqrt{\frac{1}{8}}$+$\sqrt{6}$)
=$2\sqrt{6}-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{4}-\sqrt{6}$
=$\sqrt{6}-\frac{3\sqrt{2}}{4}$;
(2)2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$÷$\sqrt{50}$.
=$4\sqrt{3}×\frac{\sqrt{3}}{4}×\frac{5\sqrt{2}}{50}$
=$\frac{3\sqrt{2}}{10}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
18.既是方程2x-y=3的解,又是方程3x-4y=2的解的是( )
| A. | $\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=4\\ y=3\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-4\\ y=-5\end{array}\right.$ |
19.若x、y为实数,且$\sqrt{2x-1}$$+\sqrt{1-2x}$+y=4,则xy的值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
3.下列说法正确的是( )
| A. | 直线a、b都经过点m | B. | 直线AB、CD都经过点M | ||
| C. | 延长射线AB到C | D. | 线段、射线、直线中,线段最短 |
20.要使$\sqrt{9+2x}$在实数范围内有意义,则( )
| A. | x为任何值 | B. | x≤-$\frac{9}{2}$ | C. | x≥$\frac{9}{2}$ | D. | x≥-$\frac{9}{2}$ |
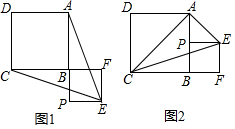 已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.