题目内容
5.设$\frac{a+b}{a-b}$=$\frac{b+c}{2(b-c)}$=$\frac{c+a}{3(c-a)}$,求8a+9b+5c的值.分析 设$\frac{a+b}{a-b}$=$\frac{b+c}{2(b-c)}$=$\frac{c+a}{3(c-a)}$=k,则a+b=k(a-b),b+c=2k(b-c),(c+a)=3k(c-a),再进一步分组分解8a+9b+5c代入求得答案即可..
解答 解:设$\frac{a+b}{a-b}$=$\frac{b+c}{2(b-c)}$=$\frac{c+a}{3(c-a)}$=k,
则a+b=k(a-b),b+c=2k(b-c),(c+a)=3k(c-a).
所以6(a+b)=6k(a-b),
3(b+c)=6k(b-c),
2(c+a)=6k(c-a).
以上三式相加,得
6(a+b)+3(b+c)+2(c+a)
=6k(a-b+b-c+c-a),
即8a+9b+5c=0.
点评 此题考查分式的化简求值,设出参数,分组分解,整体代入是解决问题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
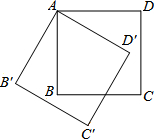 如图,将边长为2cm的正方形ABCD绕点A顺时针旋转到AB′C′D′的位置,∠B′AD=120°,则C点运动到C′点的路径长为$\frac{\sqrt{2}}{3}$πcm.
如图,将边长为2cm的正方形ABCD绕点A顺时针旋转到AB′C′D′的位置,∠B′AD=120°,则C点运动到C′点的路径长为$\frac{\sqrt{2}}{3}$πcm.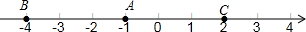 读图回答问题:
读图回答问题: