题目内容
7.在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.(1)求函数y=$\frac{4}{3}$x+4坐标三角形的三边长.
(2)若函数y=$\frac{4}{3}$x+b(b为常数)的坐标三角形的周长为24,求此三角形的面积.
分析 (1)先求函数y=$\frac{4}{3}$x+4与x、y轴的交点坐标,再求三角形的三边长;
(2)求得函数y=$\frac{4}{3}$x+b与x、y轴的交点坐标,再求三角形的三边长,把三边的长加起来等于24,解方程求解即可求得b的值,再由三角形的面积公式即可得出结论.
解答 解:(1)∵直线y=$\frac{4}{3}$x+4与x轴的交点坐标为(-3,0),与y轴交点坐标为(0,4),
∴直角三角形的斜边长=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴坐标三角形的三边长分别为:3,4,5;
(2)∵函数y=$\frac{4}{3}$x+b(b为常数)与x轴的交点坐标为(-$\frac{3b}{4}$,0),与y轴交点坐标为(0,b),
∴直角三角形的斜边长=$\sqrt{(\frac{3b}{4})^{2}+{b}^{2}}$=$\frac{5}{4}$|b|.
∵坐标三角形的周长为24,
∴|-$\frac{3b}{4}$|+|b|+|$\frac{5b}{4}$|=24,即3|b|=24,解得|b|=8,
∴S△=$\frac{1}{2}$|$\frac{3b}{4}$|•|b|=$\frac{3}{8}$b2=$\frac{3}{8}$×64=24.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
17.下列二次函数中,图象与x轴没有交点的是( )
| A. | y=3x2 | B. | y=2x2-4 | C. | y=x2-3x+5 | D. | y=x2-x-2 |
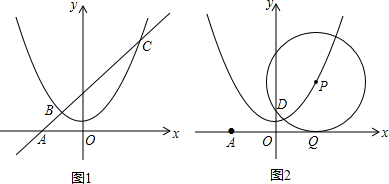
4. 如图,点C是以AB为直径的半圆型铁片上的靠近B点的一个定点,将该铁片按图中的位置斜靠在坐标轴上,现点A沿着y轴向终点O滑动,同时点B相应地沿着x轴向x轴正方向滑动,在滑动过程中,点C与原点O距离的变化情况是( )
如图,点C是以AB为直径的半圆型铁片上的靠近B点的一个定点,将该铁片按图中的位置斜靠在坐标轴上,现点A沿着y轴向终点O滑动,同时点B相应地沿着x轴向x轴正方向滑动,在滑动过程中,点C与原点O距离的变化情况是( )
 如图,点C是以AB为直径的半圆型铁片上的靠近B点的一个定点,将该铁片按图中的位置斜靠在坐标轴上,现点A沿着y轴向终点O滑动,同时点B相应地沿着x轴向x轴正方向滑动,在滑动过程中,点C与原点O距离的变化情况是( )
如图,点C是以AB为直径的半圆型铁片上的靠近B点的一个定点,将该铁片按图中的位置斜靠在坐标轴上,现点A沿着y轴向终点O滑动,同时点B相应地沿着x轴向x轴正方向滑动,在滑动过程中,点C与原点O距离的变化情况是( )| A. | 一直增大 | B. | 保持不变 | C. | 先增大后减小 | D. | 先减小后增大 |
2.下列二次根式中,是最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{6}$ | C. | $\sqrt{12}$ | D. | $\sqrt{\frac{1}{3}}$ |
 如图,已知圆环的外圆半径为46mm,内圆半径为27mm,求圆环的面积.(π取3.14,结果保留2个有效数字)
如图,已知圆环的外圆半径为46mm,内圆半径为27mm,求圆环的面积.(π取3.14,结果保留2个有效数字) 如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试分别画出一条长度是有理数的线段和一条长度是无理数的线段,并写出这两条线段的长度.
如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试分别画出一条长度是有理数的线段和一条长度是无理数的线段,并写出这两条线段的长度.