题目内容
17.下列二次函数中,图象与x轴没有交点的是( )| A. | y=3x2 | B. | y=2x2-4 | C. | y=x2-3x+5 | D. | y=x2-x-2 |
分析 分别计算△的值,来判断抛物线与x轴的交点个数.
解答 解:A、△=0-4×3×0=0,所以图象与x轴交于一点,是原点;
B、△=22-4×2×(-4)=4+32>0,所以与x轴交于两点;
C、△=(-3)2-4×1×5=9-20<0,所以图象与x轴没有交点;
D、△=(-1)2-4×1×(-2)=1+8>0,所以图象与x轴交于两点;
故选B.
点评 本题考查了抛物线与x轴的交点个数,明确△=b2-4ac决定抛物线与x轴的交点个数.①△=b2-4ac>0时,抛物线与x轴有2个交点;②△=b2-4ac=0时,抛物线与x轴有1个交点;③△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列方程是一元二次方程的是( )
| A. | x2=0 | B. | $\frac{1}{{{x^2}+2x}}$=0 | C. | x3-2x2+x-1=0 | D. | x2+2xy+2=0 |
5.下列计算正确有是( )
| A. | $2+\sqrt{2}=2\sqrt{2}$ | B. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C. | $2\sqrt{3}+3\sqrt{3}=5\sqrt{6}$ | D. | $2\sqrt{5}-3\sqrt{5}=-\sqrt{5}$ |
12.下列计算错误的是( )
| A. | $\sqrt{12}$÷$\sqrt{3}$=2 | B. | $\sqrt{8}=2\sqrt{2}$ | C. | $\sqrt{2}•\sqrt{3}$=$\sqrt{6}$ | D. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ |
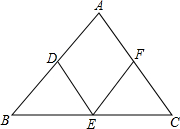 已知,如图,ADEF是菱形,AB=20cm,AC=15cm,则菱形边长$\frac{60}{7}$cm.
已知,如图,ADEF是菱形,AB=20cm,AC=15cm,则菱形边长$\frac{60}{7}$cm.