题目内容
1. 如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试分别画出一条长度是有理数的线段和一条长度是无理数的线段,并写出这两条线段的长度.
如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试分别画出一条长度是有理数的线段和一条长度是无理数的线段,并写出这两条线段的长度.
分析 连接AB,根据勾股定理,AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.故AB长度是无理数;根据勾股定理,CD=$\sqrt{{4}^{2}+{3}^{2}}$=5.故CD的长度是有理数.
解答  解:表示无理数的线段AB,表示有理数的线段CD.
解:表示无理数的线段AB,表示有理数的线段CD.
∵△ABE是直角三角形,
∴AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
同理,CD═CD=$\sqrt{{4}^{2}+{3}^{2}}$=5,
故答案为:表示无理数的线段AB,表示有理数的线段CD
点评 本题考查了无理数、有理数和勾股定理的应用,注意:在直角三角形中,两直角边的平方和等于斜边的平方.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
9.张倩同学记录了某天一天的温度变化的数据,如表所示,则温暖上升的时段是( )
| 时刻/时 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| 温度 | -3 | -5 | -6 | -4 | -3 | -1 | 0 | 1 | 0 | -1 | -2 | -4 | -4 |
| A. | 0~4时 | B. | 4~14时 | C. | 14~22时 | D. | 14~24时 |
6.某商店在出售某种商品时,以m元的价格出售,亏本20%,则在这次买卖中该商店的亏损情况是( )
| A. | 亏20%m元 | B. | 亏80%m元 | C. | 亏25%m元 | D. | 亏20%元 |
13.矩形中,对角线的性质是( )
| A. | 相等且互相垂直 | B. | 相等且互相平分 | ||
| C. | 互相垂直且平分 | D. | 互相垂直且平分内角 |
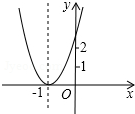 已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②4ac-b2=0;③a>2;④4a-2b+c>0.其中正确的个数是( )
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②4ac-b2=0;③a>2;④4a-2b+c>0.其中正确的个数是( )