题目内容

14．若一个直角三角形的三边长分别为a、b、c，已知a2=25，b2=144，则c2=（　　）
A．169B．119C．13或25D．169或119

分析 此题有两种情况，当a，b为直角边，c为斜边，和当a，c为直角边，b为斜边，利用勾股定理即可求解．

解答 解；当a，b为直角边时，c2=a2+b2=25+144=169，
当a，c为直角边，b为斜边时，c2=b2-a2=144-25=119，
故选：D．

点评 此题主要考查学生对勾股定理的理解和掌握，解答此题要用分类讨论的思想，学生容易忽略a，c为直角边，b为斜边时这种情况，很容易选A，因此此题是一道易错题．

练习册系列答案
相关题目
4．$\sqrt{（-3）^{2}}$的算术平方根是（　　）
A．±3B．3C．$±\sqrt{3}$D．$\sqrt{3}$
5．计算：
（1）-20+（-17）-（-18）-11；       
（2）23-6×（-3）2+2×（-4）；
（3）-1.53×0.75+0.53×$\frac{3}{4}$-3.4×0.75； 
（4）54÷$\frac{3}{4}$-（-54）÷$\frac{1}{2}$+54÷（-$\frac{1}{4}$）．
2．做重复试验：抛掷一枚啤酒瓶盖1000次．经过统计得“凸面向上”的次数为420次，则可以由此估计抛掷这枚啤酒瓶盖出现“凸面向上”的概率约为（　　）
A．0.22B．0.42C．0.50D．0.58
9．已知方程组$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=m+1}\\{xy=m-1}\end{array}\right.$ 有实数解，求实数m的取值范围．
19．甲、乙两城市为了解决空气质量污染问题，对城市及其周边的环境污染进行了综合治理．在治理的过程中，环保部门每月初对两城市的空气质量进行监测，连续10个月的空气污染指数如图所示．其中，空气污染指数≤50时，空气质量为优；50＜空气污染指数≤100时，空气质量为良；100＜空气污染指数≤150时，空气质量为轻微污染．

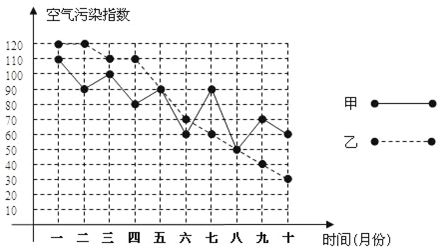
（1）填写下表：
平均数方差中位数空气质量为优的次数
甲803401
乙1060803
（2）从以下四个方面对甲、乙两城市的空气质量进行分析．
①从平均数和空气质量为优的次数来分析：空气质量为优的次数甲城市比乙城市少；（填“多”或“少），乙城市的空气质量比甲城市的空气质量好些．（填“好些”或“差些”）；
②从平均数和中位数来分析：甲的中位数＜乙的中位数（填“=”、“＞”或“＜”），空气质量相对较好的城市是乙（填“甲”或“乙”）；
③从平均数和方差来分析：S甲2＜S乙2，空气污染指数比较稳定的城市是甲（填“甲”或“乙”）；
④根据折线图上两城市的空气污染指数的走势来分析，两城市治理环境污染的效果较好的城市是乙（填“甲”或“乙”）．
6．下列计算正确的是（　　）
A．a6÷a3=a2B．（a3）2=a5C．（ab）3=ab3D．a•a2=a3
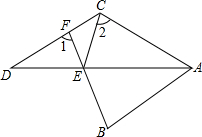3．多项式（4xy-3x2-xy+x2+y2）-（3xy-2x2+2y2）的值与x无关．（填“x”或“y”）
8．如图，AD平分∠BAC，∠BAC+∠ACD=180°，E在AD上，BE的延长线交CD于F，连CE，且∠1=∠2，求证：AB=AC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网