题目内容
10．
如图，四边形ABCD是平行四边形，E，F分别为BC，AD的中点，（1）求证：AE=CF；
（2）延长CF交BA的延长线于点M，求证：AM=AB．
分析 （1）只要证明AF=CE，AF∥CE即可解决问题；
（2）根据平行线分线段成比例定理即可证明；
解答 证明：（1）∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，
又∵E，F分别为BC，AD的中点，
∴AF=$\frac{1}{2}$AD，CE=$\frac{1}{2}$BC，
∴AF=CE，
∴四边形AECF是平行四边形，
∴AE=CF．
（2）∵四边形AECF是平行四边形，
∴AE∥CF，
又∵E为BC的中点，
∴A为BM的中点，
即AM=AB．
点评 本题考查平行四边形的性质和判定、平行线分线段成比例定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
将面积为$\sqrt{3}$cm2的等边三角形绕点O按顺时针方向依次旋转60°后得如图，则该图形的边长是2cm，图中共有6个平行四边形．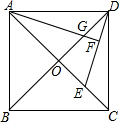
如图，正方形ABCD的两条对角线相交于点O．点E是OC的中点，连接DE，过点A作AF⊥DE于点F，交OD于点G．若正方形的边长为4$\sqrt{2}$，则DF=$\frac{4\sqrt{5}}{5}$．
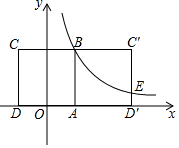如图，边长为2的正方形ABCD关于y轴对称，边AD在x轴上，点B在第一象限，反比例函数y=$\frac{k}{x}$的图象经过点B，将正方形ABCD沿边AB翻折得到正方形ABC′D′，C′D′与y=$\frac{k}{x}$的图象交于点E．
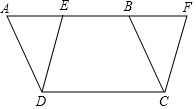如图，在平行四边形ABCD中，点E是AB边上任意一点，连接DE．过点C作线段DE的平行线，交AB延长线于点F．
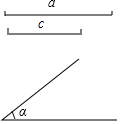尺规作图，已知线段a、线段c和∠α，用直尺和圆规作△ABC，使BC=a，AB=c，∠ABC=∠α．（要求画出图形，并保留作图痕迹，不必写作法）