题目内容
16．已知CD为Rt△ABC斜边上的高，AC：BC=3：2，如果S△ADC=9，那么S△BDC=4．分析 由题可知：△ACD∽△CBD，则可知相似比，然后根据相似比求解．
解答 解：∵CD为Rt△ABC斜边上的高，
∴△ACD∽△CBD，
∵AC：BC=3：2，
∴面积的比是9：4，
即S△ADC：S△CBD=9：4，
∴S△BDC=4．
故答案为4．
点评 本题主要考查了相似三角形的面积的比等于相似比的平方．
练习册系列答案
教材全解字词句篇系列答案
相关题目
6．若a＞b，则下列式子正确的是（ ）
| A． | a-2＞b-2 | B． | $\frac{1}{2}$a＜$\frac{1}{2}$b | C． | 4+3a＜4+3b | D． | -2a＞-2b |
如图，Rt△ABC中，∠B=90°，BC=5$\sqrt{3}$，∠C=30°，点D从点C出发沿CA方向以每秒2个单位长度的速度向点A运动．同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B运动．当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F．联结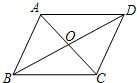
如图，四边形ABCD的对角线交于点O，AB∥CD，O是BD的中点．
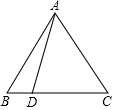如图，已知等边△ABC的边长为2，D为BC上一点，且∠DAC=45°，则△ABD的面积为2$\sqrt{3}$-3．
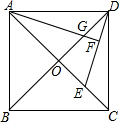如图，正方形ABCD的两条对角线相交于点O．点E是OC的中点，连接DE，过点A作AF⊥DE于点F，交OD于点G．若正方形的边长为4$\sqrt{2}$，则DF=$\frac{4\sqrt{5}}{5}$．
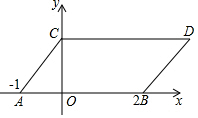如图，在平面直角坐标系中，点A，B的坐标分别为（-1，0），（2，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．