题目内容
14.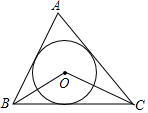 如图,在△ABC中,点O是△ABC的内心,∠BOC=118°,∠A=56°.
如图,在△ABC中,点O是△ABC的内心,∠BOC=118°,∠A=56°.
分析 先根据∠BOC=118°求出∠OBC+∠OCB的度数,再由角平分线的性质求出∠ABC+∠ACB的度数,由三角形内角和定理即可得出结论.
解答 解:∵∠BOC=118°,
∴∠OBC+∠OCB=180°-118°=62°.
∵点O是△ABC的∠ABC与∠ACB两个角的角平分线的交点,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=124°,
∴∠A=180°-124°=56°.
故答案为:56.
点评 本题考查的是三角形的内切圆与内心,三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
19.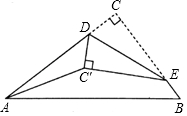 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,点D、E分别在AC、BC上.现将△DCE沿DE翻折,使点C落在点C'处.连接AC',则AC'长度的最小值.( )
如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,点D、E分别在AC、BC上.现将△DCE沿DE翻折,使点C落在点C'处.连接AC',则AC'长度的最小值.( )
 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,点D、E分别在AC、BC上.现将△DCE沿DE翻折,使点C落在点C'处.连接AC',则AC'长度的最小值.( )
如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,点D、E分别在AC、BC上.现将△DCE沿DE翻折,使点C落在点C'处.连接AC',则AC'长度的最小值.( )| A. | 不存在 | B. | 等于1cm | C. | 等于2 cm | D. | 等于2.5 cm |
4.已知-x+y=3,则2(x-y)2-4(x-y)+6的值是( )
| A. | 9 | B. | 12 | C. | -15 | D. | 36 |
 如图,AB=2BC,D为AC的中点,DC=3cm,求AB的长.
如图,AB=2BC,D为AC的中点,DC=3cm,求AB的长. 有理数a、b在数轴上的位置如图所示,试化简:|a|-|a+b|=b.
有理数a、b在数轴上的位置如图所示,试化简:|a|-|a+b|=b.