题目内容
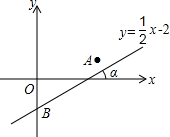 如图,直线y=
如图,直线y=| 1 |
| 2 |
(1)OA,OB的长;
(2)tanα与sinα的值.
考点:一次函数图象上点的坐标特征,解直角三角形
专题:
分析:(1)先根据题意求出AB两点的坐标,进而可得出结论;
(2)根据勾股定理求出AB的值,根据锐角三角函数的定义即可得出结论.
(2)根据勾股定理求出AB的值,根据锐角三角函数的定义即可得出结论.
解答:解:(1)∵直线y=
x-2交x轴于点A,交y轴于点B,
∴A(4,0),B(0,-2),
∴OA=4,OB=2;
(2)∵OA=4,OB=2,
∴AB=
=2
,
∵∠α=∠OAB,
∴tanα=
=
=
,
sinα=
=
=
.
| 1 |
| 2 |
∴A(4,0),B(0,-2),
∴OA=4,OB=2;
(2)∵OA=4,OB=2,
∴AB=
| 42+22 |
| 5 |
∵∠α=∠OAB,
∴tanα=
| OB |
| OA |
| 2 |
| 4 |
| 1 |
| 2 |
sinα=
| OB |
| AB |
| 2 | ||
2
|
| ||
| 5 |
点评:本题考查的是一次函数图象上点的坐标特点,熟知坐标轴上各点的坐标特点是解答此题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,在Rt△ABC中,∠B=30°,BD=AD,BD=12,求BC的长.
如图,在Rt△ABC中,∠B=30°,BD=AD,BD=12,求BC的长. 如图,在?ABCD中,对角线AC,BD交于点O,且E,F分别是BO和DO的中点.求证:AE=CF.
如图,在?ABCD中,对角线AC,BD交于点O,且E,F分别是BO和DO的中点.求证:AE=CF.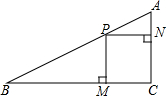 如图,在Rt△ABC中,点P在斜边AB上移动,PM⊥BC,PN⊥AC,M,N分别为垂足,AC=1,AB=2,则何时矩形PMCN的面积最大?最大面积是多少?
如图,在Rt△ABC中,点P在斜边AB上移动,PM⊥BC,PN⊥AC,M,N分别为垂足,AC=1,AB=2,则何时矩形PMCN的面积最大?最大面积是多少?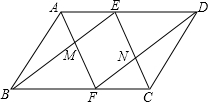 如图,已知在平行四边形ABCD中,E,F为边AD,BC上的点,且AE=CF,连接AF,EC,BE,DF交于M,N,试判断MF与NE的关系,并证明你的结论.
如图,已知在平行四边形ABCD中,E,F为边AD,BC上的点,且AE=CF,连接AF,EC,BE,DF交于M,N,试判断MF与NE的关系,并证明你的结论.