Question

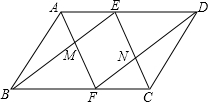如图，已知在平行四边形ABCD中，E，F为边AD，BC上的点，且AE=CF，连接AF，EC，BE，DF交于M，N，试判断MF与NE的关系，并证明你的结论．

Answer 1

考点：平行四边形的判定与性质

专题：

分析：MF=NE，且MF∥NE．平行四边形性质里有的对边互相平行，判定里面有若是四边形的对边平行且相等那么就是平行四边形，根据判定定理和性质定理，此问题得证．

解答：解：MF=NE，且MF∥NE．理由如下：
∵四边形ABCD是平行四边形，则AD∥BC．
∵AE=CF，
∴DE

∥

.

BF，
∴四边形BEDF是平行四边形，
∴BE∥DF，即ME∥FN．
∵AE

∥

.

CF，
∴四边形AECF是平行四边形，
∴MF∥EN，
∴四边形MENF是平行四边形，
∴MF=NE，且MF∥NE．

点评：本题考查平行四边形的判定和性质定理，关键知道性质里有的对边互相平行，判定里面有若是四边形的对边平行且相等那么就是平行四边形．