题目内容
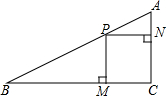 如图,在Rt△ABC中,点P在斜边AB上移动,PM⊥BC,PN⊥AC,M,N分别为垂足,AC=1,AB=2,则何时矩形PMCN的面积最大?最大面积是多少?
如图,在Rt△ABC中,点P在斜边AB上移动,PM⊥BC,PN⊥AC,M,N分别为垂足,AC=1,AB=2,则何时矩形PMCN的面积最大?最大面积是多少?考点:相似三角形的判定与性质,二次函数的最值
专题:
分析:设PA=x 矩形PMCN的面积为y 则BP=AB-AP=2-x,由勾股定理可求出BC的长,再根据相似三角形的性质可得到PM,PN的值,根据矩形的面积公式计算即可.
解答:解:设PA=x 矩形PMCN的面积为y 则BP=AB-AP=2-x,
在直角△ABC中:∵AC=1 AB=2,
∴BC=
,
∵PM⊥BC,PN⊥AC,
∴PM‖AC,PN‖BC,
∴
=
,
=
,
∴
=
,
=
,
∴PM=
,PN=
,
∴y=PM×PN=
×
x=
(2x-x2),
=-
(x-1)2+
∴当x=1时,即PA=1,P是AB的中点时矩形PMCN的面积最大,最大面积是
.
在直角△ABC中:∵AC=1 AB=2,
∴BC=
| 3 |
∵PM⊥BC,PN⊥AC,
∴PM‖AC,PN‖BC,
∴
| PM |
| AC |
| BP |
| BA |
| PA |
| AB |
| PN |
| BC |
∴
| PM |
| 1 |
| 2-x |
| 2 |
| x |
| 2 |
| PN | ||
|
∴PM=
| 2-x |
| 2 |
| ||
| 2 |
∴y=PM×PN=
| 2-x |
| 2 |
| ||
| 2 |
| ||
| 4 |
=-
| ||
| 4 |
| ||
| 4 |
∴当x=1时,即PA=1,P是AB的中点时矩形PMCN的面积最大,最大面积是
| ||
| 4 |
点评:本题考查了勾股定理的逆定理的运用,相似三角形的判定与性质,矩形的面积公式的运用,二次函数的顶点式的运用及最值的确定.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,直线y=
如图,直线y=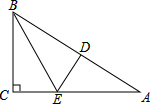 如图,在Rt△ABC中,∠C=90°,沿过B点的一直线BE折叠这个三角形,使点C与AB边上的一点D重合.当∠A满足什么条件时,点D恰好为AB的中点?写出一个你认为适当的条件,并利用此条件证明D为AB的中点.
如图,在Rt△ABC中,∠C=90°,沿过B点的一直线BE折叠这个三角形,使点C与AB边上的一点D重合.当∠A满足什么条件时,点D恰好为AB的中点?写出一个你认为适当的条件,并利用此条件证明D为AB的中点.