题目内容
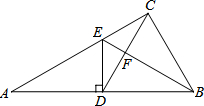 如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,过D作DE⊥AB交AC于点E,CE=DE.连接CD交BE于点F.
如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,过D作DE⊥AB交AC于点E,CE=DE.连接CD交BE于点F.(1)求证:BC=BD;
(2)若点D为AB的中点,求∠AED的度数.
考点:全等三角形的判定与性质
专题:
分析:(1)直接证明Rt△DEB≌Rt△CEB,即可解决问题.
(2)首先证明△ADE≌△BDE,进而证明∠AED=∠DEB=∠CEB,即可解决问题.
(2)首先证明△ADE≌△BDE,进而证明∠AED=∠DEB=∠CEB,即可解决问题.
解答: 证明:(1)∵DE⊥AB,∠ACB=90°,
证明:(1)∵DE⊥AB,∠ACB=90°,
∴△DEB与△CEB都是直角三角形,
在△DEB与△CEB中,
,
∴Rt△DEB≌Rt△CEB(HL),
∴BC=BD.
(2)∵DE⊥AB,
∴∠ADE=∠BDE=90°;
∵点D为AB的中点,
∴AD=BD;
在△ADE与△BDE中,
,
∴△ADE≌△BDE(SAS),
∴∠AED=∠DEB;
∵△DEB≌△CEB,
∴∠CEB=∠DEB,
∴∠AED=∠DEB=∠CEB;
∵∠AED+∠DEB+∠CEB=180°,
∴∠AED=60°.
 证明:(1)∵DE⊥AB,∠ACB=90°,
证明:(1)∵DE⊥AB,∠ACB=90°,∴△DEB与△CEB都是直角三角形,
在△DEB与△CEB中,
|
∴Rt△DEB≌Rt△CEB(HL),
∴BC=BD.
(2)∵DE⊥AB,
∴∠ADE=∠BDE=90°;
∵点D为AB的中点,
∴AD=BD;
在△ADE与△BDE中,
|
∴△ADE≌△BDE(SAS),
∴∠AED=∠DEB;
∵△DEB≌△CEB,
∴∠CEB=∠DEB,
∴∠AED=∠DEB=∠CEB;
∵∠AED+∠DEB+∠CEB=180°,
∴∠AED=60°.
点评:该命题以三角形为载体,以考查全等三角形的判定及其应用为核心构造而成;解题的关键是灵活运用全等三角形的判定及其性质,来分析、判断或推理.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 如图是一次函数y=kx+b的图象,当1<y<2时,x的取值范围是( )
如图是一次函数y=kx+b的图象,当1<y<2时,x的取值范围是( )| A、x<2 | B、1<x<2 |
| C、2<x<3 | D、x>3 |
 如图所示,已知ABC中,AB=AC,AD⊥BC于D,BE、CF交AD于H,则图中全等三角形有
如图所示,已知ABC中,AB=AC,AD⊥BC于D,BE、CF交AD于H,则图中全等三角形有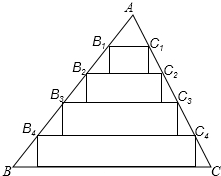 给一版墙镶边,需要4cm宽的彩色纸条48cm.现有如图一张三角形彩色纸零件,其中BC=25cm,BC边上的高线长为20cm.小慧给出一种裁纸方法:如图,将AB、AC分别五等分,然后连结两边对应的点,并以这些连结线为一边作矩形.剪下矩形纸条作为墙报镶边的材料.问:小慧的这种方法能满足这版墙报镶边的需要吗?请说明理由.
给一版墙镶边,需要4cm宽的彩色纸条48cm.现有如图一张三角形彩色纸零件,其中BC=25cm,BC边上的高线长为20cm.小慧给出一种裁纸方法:如图,将AB、AC分别五等分,然后连结两边对应的点,并以这些连结线为一边作矩形.剪下矩形纸条作为墙报镶边的材料.问:小慧的这种方法能满足这版墙报镶边的需要吗?请说明理由.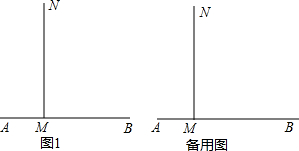 已知:如图1,射线MN⊥AB,点C从M出发,沿射线MN运动,AM=1,MB=4.
已知:如图1,射线MN⊥AB,点C从M出发,沿射线MN运动,AM=1,MB=4. 已知:如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,AD=AE.求证:AB=AC.
已知:如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,AD=AE.求证:AB=AC.