题目内容
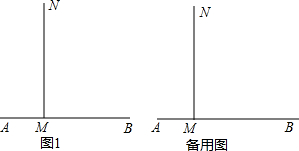 已知:如图1,射线MN⊥AB,点C从M出发,沿射线MN运动,AM=1,MB=4.
已知:如图1,射线MN⊥AB,点C从M出发,沿射线MN运动,AM=1,MB=4.(1)当△ABC为等腰三角形时,求MC的长;
(2)当△ABC为直角三角形时,求MC的长;
(3)点C在运动的过程中,若△ABC为钝角三角形,则MC的长度范围
考点:勾股定理,线段垂直平分线的性质
专题:动点型
分析:(1)如图1,分CB=AB,AB=AC,AC=BC三种情况进行讨论即可;
(2)当∠ACB=90°时,由勾股定理得AC2+BC2=AB2,在Rt△MCA中,由勾股定理得:AC2=AM2+CM2;在Rt△MCB中,由勾股定理得:BC2=BM2+CM2,故AM2+CM2+BM2+CM2=AB2,由此可得出CM的长;
(3)根据(2)中CM的长即可得出结论.
(2)当∠ACB=90°时,由勾股定理得AC2+BC2=AB2,在Rt△MCA中,由勾股定理得:AC2=AM2+CM2;在Rt△MCB中,由勾股定理得:BC2=BM2+CM2,故AM2+CM2+BM2+CM2=AB2,由此可得出CM的长;
(3)根据(2)中CM的长即可得出结论.
解答: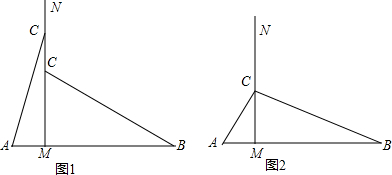 解:(1)如图1,
解:(1)如图1,
当CB=AB时,在Rt△MCB,
∵MB=4,AM=1,
∴AB=5,
∴CM=
=3;
当AB=AC时,
在Rt△MCA,
CM=
=
;
当AC=BC时,C在AB的垂直平分线上,与条件不合.
(2)如图,∵当∠ACB=90°时,由勾股定理得AC2+BC2=AB2,
又∵在Rt△MCA,由勾股定理得:AC2=AM2+CM2,
在Rt△MCB由勾股定理得:BC2=BM2+CM2,
∴AM2+CM2+BM2+CM2=AB2,
∵AM=1,MB=4,AB=5,
∴CM2+16=25,解得CM=2;
(3)∵由(2)得,当CM=2时,△ABC是直角三角形,
∴0<CM<2时,△ABC为钝角三角形;当CM>2时,△ABC为锐角三角形.
故答案为:0<CM<2,CM>2.
 解:(1)如图1,
解:(1)如图1,当CB=AB时,在Rt△MCB,
∵MB=4,AM=1,
∴AB=5,
∴CM=
| 52-42 |
当AB=AC时,
在Rt△MCA,
CM=
| 52-12 |
| 24 |
当AC=BC时,C在AB的垂直平分线上,与条件不合.
(2)如图,∵当∠ACB=90°时,由勾股定理得AC2+BC2=AB2,
又∵在Rt△MCA,由勾股定理得:AC2=AM2+CM2,
在Rt△MCB由勾股定理得:BC2=BM2+CM2,
∴AM2+CM2+BM2+CM2=AB2,
∵AM=1,MB=4,AB=5,
∴CM2+16=25,解得CM=2;
(3)∵由(2)得,当CM=2时,△ABC是直角三角形,
∴0<CM<2时,△ABC为钝角三角形;当CM>2时,△ABC为锐角三角形.
故答案为:0<CM<2,CM>2.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
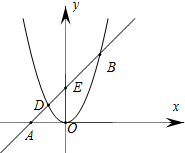 已知一次函数y=x+2与二次函数y=x2交于点D与B,y=x+2与x轴、y轴的交点分别为点A与点B,求S△ODB的值.
已知一次函数y=x+2与二次函数y=x2交于点D与B,y=x+2与x轴、y轴的交点分别为点A与点B,求S△ODB的值.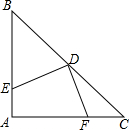 Rt△ABC中,AB=AC=2,∠A=90°,D为BC中点,点E,F分别在AB,AC上,且BE=AF,
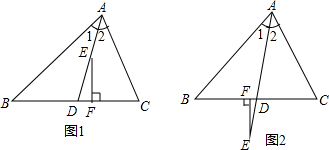
Rt△ABC中,AB=AC=2,∠A=90°,D为BC中点,点E,F分别在AB,AC上,且BE=AF,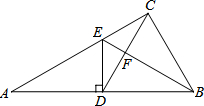 如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,过D作DE⊥AB交AC于点E,CE=DE.连接CD交BE于点F.
如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,过D作DE⊥AB交AC于点E,CE=DE.连接CD交BE于点F. 如图:已知AB,CD相交于点O,且AB=DC,AC=DB,求证:∠A=∠D.
如图:已知AB,CD相交于点O,且AB=DC,AC=DB,求证:∠A=∠D.