题目内容
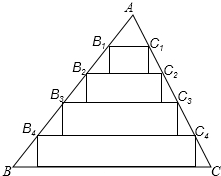 给一版墙镶边,需要4cm宽的彩色纸条48cm.现有如图一张三角形彩色纸零件,其中BC=25cm,BC边上的高线长为20cm.小慧给出一种裁纸方法:如图,将AB、AC分别五等分,然后连结两边对应的点,并以这些连结线为一边作矩形.剪下矩形纸条作为墙报镶边的材料.问:小慧的这种方法能满足这版墙报镶边的需要吗?请说明理由.
给一版墙镶边,需要4cm宽的彩色纸条48cm.现有如图一张三角形彩色纸零件,其中BC=25cm,BC边上的高线长为20cm.小慧给出一种裁纸方法:如图,将AB、AC分别五等分,然后连结两边对应的点,并以这些连结线为一边作矩形.剪下矩形纸条作为墙报镶边的材料.问:小慧的这种方法能满足这版墙报镶边的需要吗?请说明理由.考点:相似三角形的应用
专题:
分析:求出△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4,推出
=
=
,
=
=
,
=
=
,
=
=
,求出B1C1=5,B2C2=10,B3C3=15,B4C4=20,根据已知判断即可.
| B1C1 |
| BC |
| AE |
| AM |
| 1 |
| 5 |
| B2C2 |
| BC |
| AH |
| AM |
| 2 |
| 5 |
| B3C3 |
| BC |
| AG |
| AM |
| 3 |
| 5 |
| B4C4 |
| BC |
| AN |
| AM |
| 4 |
| 5 |
解答: 解:小慧的这种方法不能满足这版墙报镶边的需要,
解:小慧的这种方法不能满足这版墙报镶边的需要,
理由:过A作AM⊥BC于M,交B1C1于E,交B2C2于H,交B3C3于G,交B4C4于N,则AM⊥B4C4,AM⊥B3C3,AM⊥B2C2,AM⊥B1C1,
∵由矩形的性质得:BC∥B1C1∥B2C2∥B3C3∥B4C4,
∴△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4,
=
=
,
=
=
,
=
=
,
=
=
,
∵AM=20,BC=25,
∴B1C1=5,B2C2=10,B3C3=15,B4C4=20,
∵B1C1+B2C2+B3C3+B4C4=5+10+15+20=50>48,
∴小慧的这种方法不能满足这版墙报镶边的需要.
 解:小慧的这种方法不能满足这版墙报镶边的需要,
解:小慧的这种方法不能满足这版墙报镶边的需要,理由:过A作AM⊥BC于M,交B1C1于E,交B2C2于H,交B3C3于G,交B4C4于N,则AM⊥B4C4,AM⊥B3C3,AM⊥B2C2,AM⊥B1C1,
∵由矩形的性质得:BC∥B1C1∥B2C2∥B3C3∥B4C4,
∴△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4,
| B1C1 |
| BC |
| AE |
| AM |
| 1 |
| 5 |
| B2C2 |
| BC |
| AH |
| AM |
| 2 |
| 5 |
| B3C3 |
| BC |
| AG |
| AM |
| 3 |
| 5 |
| B4C4 |
| BC |
| AN |
| AM |
| 4 |
| 5 |
∵AM=20,BC=25,
∴B1C1=5,B2C2=10,B3C3=15,B4C4=20,
∵B1C1+B2C2+B3C3+B4C4=5+10+15+20=50>48,
∴小慧的这种方法不能满足这版墙报镶边的需要.
点评:本题考查了相似三角形的性质和判定和矩形的性质的应用,注意:相似三角形的对应高的比等于相似比.

练习册系列答案
相关题目
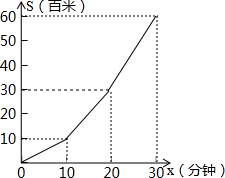 小明利用星期六、日双休骑自行车到城外小姨家去玩,星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家,行程情况如图所示.星期日小明又沿原路返回自己家中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是( )
小明利用星期六、日双休骑自行车到城外小姨家去玩,星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家,行程情况如图所示.星期日小明又沿原路返回自己家中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是( )| A、30分钟 | ||
B、38
| ||
C、41
| ||
D、43
|
 实数a,b,c在数轴上的对应点的位置如图所示,化简|b-c|+|c-a|-|b|-|a+c|的结果是
实数a,b,c在数轴上的对应点的位置如图所示,化简|b-c|+|c-a|-|b|-|a+c|的结果是 已知:如图,CB=DE,∠B=∠E,∠BAE=∠CAD.
已知:如图,CB=DE,∠B=∠E,∠BAE=∠CAD.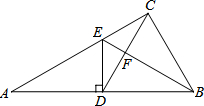 如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,过D作DE⊥AB交AC于点E,CE=DE.连接CD交BE于点F.
如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,过D作DE⊥AB交AC于点E,CE=DE.连接CD交BE于点F. 如图,将△ABC放在每个小正方形面积为1的网格中,点A、B、C均落在格点上,则△ABC的面积为
如图,将△ABC放在每个小正方形面积为1的网格中,点A、B、C均落在格点上,则△ABC的面积为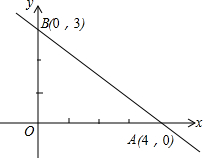 如图,直线y=-
如图,直线y=-