题目内容
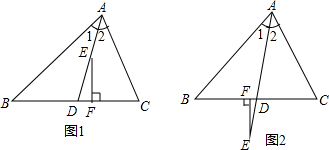
 已知:如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,AD=AE.求证:AB=AC.
已知:如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,AD=AE.求证:AB=AC.考点:全等三角形的判定与性质
专题:证明题
分析:观察图形,可以发现△ABE≌△ACD,即可解决问题.
解答: 证明:∵CD⊥AB,BE⊥AC
证明:∵CD⊥AB,BE⊥AC
∴∠ADC=∠AEB=90°,
在△ABE与△ACD中,
,
∴△ABE≌△ACD(ASA),
∴AB=AC.
 证明:∵CD⊥AB,BE⊥AC
证明:∵CD⊥AB,BE⊥AC∴∠ADC=∠AEB=90°,
在△ABE与△ACD中,
|
∴△ABE≌△ACD(ASA),
∴AB=AC.
点评:该命题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是结合图形,准确找出图形中隐含的全等三角形.

练习册系列答案
相关题目
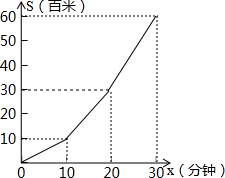 小明利用星期六、日双休骑自行车到城外小姨家去玩,星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家,行程情况如图所示.星期日小明又沿原路返回自己家中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是( )
小明利用星期六、日双休骑自行车到城外小姨家去玩,星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家,行程情况如图所示.星期日小明又沿原路返回自己家中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是( )| A、30分钟 | ||
B、38
| ||
C、41
| ||
D、43
|
 如图,如图△ABE≌△DCE,AE=2cm,BE=1.2cm,∠A=25°,∠B=48°,那么DE=
如图,如图△ABE≌△DCE,AE=2cm,BE=1.2cm,∠A=25°,∠B=48°,那么DE=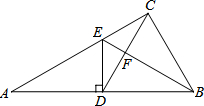 如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,过D作DE⊥AB交AC于点E,CE=DE.连接CD交BE于点F.
如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,过D作DE⊥AB交AC于点E,CE=DE.连接CD交BE于点F. 如图,将△ABC放在每个小正方形面积为1的网格中,点A、B、C均落在格点上,则△ABC的面积为
如图,将△ABC放在每个小正方形面积为1的网格中,点A、B、C均落在格点上,则△ABC的面积为