题目内容
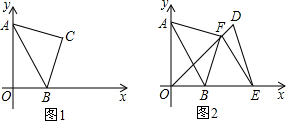
14. 如图,△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,则∠AEB的度数是( )
如图,△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,则∠AEB的度数是( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
分析 先由等边三角形的性质,判断出∠ACD=∠BCE,再用SAS判定△ACD≌△BCE,进而得到得到∠ADC=∠BEC,再用邻补角求出∠AEB的度数.
解答 解:∵△ACB和△DCE均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠ADC=∠BEC,
∵∠ADC+∠CDE=180°,∠CDE=60°,
∴∠ADC=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC-∠CED=120°-60°=60°.
故选:C.
点评 此题主要考查了等边三角形的性质,邻补角以及全等三角形的判定与性质的综合应用,解题的关键是根据全等三角形的对应角相等得到∠ADC=∠BEC.

练习册系列答案
相关题目
9.下列表格是二次函数y=ax2+bx+c(d≠0)的自变量x与函数y的一些对应值,由此可以判断方程ax2+bx+c=0(a≠0)的一个根在( )
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | -0.03 | -0.01 | 0.02 | 0.06 |
| A. | -0.01-0.02之间 | B. | 0.02-0.06之间 | C. | 6.17-6.18之间 | D. | 6.18-6.19之间 |
6.2016年5月3日中国日报网报道,科学家发现了三颗类地行星,这一发现为寻找外星生命提供了最好的机会,若某类地行星的体积V为2.88×1011π立方千米,则该类地行星的半径r为(V=$\frac{4}{3}$πr3)( )
| A. | 4×103千米 | B. | 6×103千米 | C. | 8×103千米 | D. | 6×104千米 |
 如图,一座拱桥的轮廓是抛物线型,当拱顶离水面2m时,水面宽4m,则水面下降1m时,水面宽度增加2$\sqrt{6}$-4m.
如图,一座拱桥的轮廓是抛物线型,当拱顶离水面2m时,水面宽4m,则水面下降1m时,水面宽度增加2$\sqrt{6}$-4m.