题目内容
3. 如图,一座拱桥的轮廓是抛物线型,当拱顶离水面2m时,水面宽4m,则水面下降1m时,水面宽度增加2$\sqrt{6}$-4m.
如图,一座拱桥的轮廓是抛物线型,当拱顶离水面2m时,水面宽4m,则水面下降1m时,水面宽度增加2$\sqrt{6}$-4m.
分析 根据已知得出直角坐标系,进而求出二次函数解析式,再通过把y=-1代入抛物线解析式得出水面宽度,即可得出答案.
解答 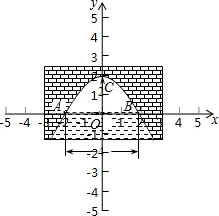 解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),
通过以上条件可设顶点式y=ax2+2,其中a可通过代入A点坐标(-2,0),
到抛物线解析式得出:a=-0.5,所以抛物线解析式为y=-0.5x2+2,
当水面下降1米,通过抛物线在图上的观察可转化为:
当y=-1时,对应的抛物线上两点之间的距离,也就是直线y=-1与抛物线相交的两点之间的距离,
可以通过把y=-1代入抛物线解析式得出:
-1=-0.5x2+2,
解得:x=±$\sqrt{6}$,所以水面宽度增加到2$\sqrt{6}$米,比原先的宽度增加了2$\sqrt{6}$-4.
故答案为:2$\sqrt{6}$-4.
点评 此题主要考查了二次函数的应用,根据已知建立坐标系从而得出二次函数解析式是解决问题的关键.

练习册系列答案
相关题目
14. 如图,△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,则∠AEB的度数是( )
如图,△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,则∠AEB的度数是( )
 如图,△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,则∠AEB的度数是( )
如图,△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,则∠AEB的度数是( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
11.已知关于x的一元一次方程2x-a=0的解是x=1,则a的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
18.在平面直角坐标系中,已知点A(0,1),B(4,2),以原点O为位似中心,把△OAB按相似比1:2缩小,则点B的对应点B′的坐标是( )
| A. | (2,1) | B. | (-2,1) | C. | (2,1)或(-2,1) | D. | (2,1)或(-2,-1) |
15.下列长度的三条线段能组成三角形的是( )
| A. | 2,3,4 | B. | 3,3,6 | C. | 1,2,3 | D. | 5,10,4 |
12.下列调查中,最合适采用普查方式的是( )
| A. | 调查一批汽车的使用寿命 | |
| B. | 调查山东省市民春节期间计划外出旅游情况 | |
| C. | 调查某航班的旅客是否携带了违禁物品 | |
| D. | 调查全国初三学生的视力情况 |