题目内容
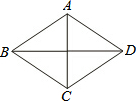 如图,在菱形ABCD中,AC=6,BD=8.
如图,在菱形ABCD中,AC=6,BD=8.(1)求sin∠ABD.
(2)扬扬发现∠ABC=2∠ABD,于是她推测:sin∠ABC=2sin∠ABD,它的推测正确吗?请通过本题图形中的数据予以说明.
考点:菱形的性质,勾股定理,解直角三角形
专题:
分析:(1)由菱形的性质可得AC⊥BD,AO=3,BO=4,△ABO是直角三角形,再利用勾股定理可得到AB=5,再利用正弦的定义即可求得sin∠ABD的值;
(2)作AE⊥BC,构筑直角三角形ABE,利用平行四边形的面积求得AE的长度,再在直角三角形ABE中,利用正弦的定义即可求得sin∠ABC,从而可证sin∠ABC与2sin∠ABD不相等.
(2)作AE⊥BC,构筑直角三角形ABE,利用平行四边形的面积求得AE的长度,再在直角三角形ABE中,利用正弦的定义即可求得sin∠ABC,从而可证sin∠ABC与2sin∠ABD不相等.
解答:解:(1)设AC、BD交于点O,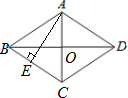
则AO⊥BO,AO=3,BO=4,
根据勾股定理得AB=
=5,
∴sin∠ABD=
.
(2)不正确.
理由:如图,作AE⊥BC,垂足为E,菱形ABCD的面积=
AC×BD=BC×AE,
即
×6×8=5×AE,
得AE=
,
所以sin∠ABC=
=
=
.
由(1)得sin∠ABD=
,
∴2sin∠ABD=2×
=
≠sin∠ABC,
即扬扬的推测不正确.

则AO⊥BO,AO=3,BO=4,
根据勾股定理得AB=
| 32+42 |
∴sin∠ABD=
| 3 |
| 5 |
(2)不正确.
理由:如图,作AE⊥BC,垂足为E,菱形ABCD的面积=
| 1 |
| 2 |
即
| 1 |
| 2 |
得AE=
| 24 |
| 5 |
所以sin∠ABC=
| AE |
| AB |
| ||
| 5 |
| 24 |
| 25 |
由(1)得sin∠ABD=
| 3 |
| 5 |
∴2sin∠ABD=2×
| 3 |
| 5 |
| 6 |
| 5 |
即扬扬的推测不正确.
点评:本题主要考查菱形的性质,面积公式及锐角三角函数中正弦的定义,掌握好菱形的性质和正弦定义是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
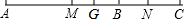 如图,G是AC的中点,M是AB的中点,N是BC的中点,那么下列四个等式中,不成立的是( )
如图,G是AC的中点,M是AB的中点,N是BC的中点,那么下列四个等式中,不成立的是( )| A、MN=GC | ||
B、MG=
| ||
C、GN=
| ||
D、MN=
|
下列说法中正确的是( )
| A、数轴上距离原点2个单位长度的点表示的数是2 |
| B、-1是最大的负整数 |
| C、任何有理数的绝对值都大于0 |
| D、0是最小的有理数 |
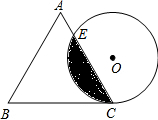 如图,边长为4cm的等边三角形ABC与⊙O等高(即高与直径相等),⊙O与BC相切于点C,⊙O与AC相交于E.
如图,边长为4cm的等边三角形ABC与⊙O等高(即高与直径相等),⊙O与BC相切于点C,⊙O与AC相交于E. 如图,点D是△ABC中BC边上的中点,连接AD并延长使DE=AD,连接BE.请指出图中成中心对称的线段、三角形,并写出面积相等的三角形.
如图,点D是△ABC中BC边上的中点,连接AD并延长使DE=AD,连接BE.请指出图中成中心对称的线段、三角形,并写出面积相等的三角形.