题目内容
平面直角坐标系中,O为原点,已知A(-2,4)、B(4,1),则△AOB面积为 .
考点:坐标与图形性质,三角形的面积
专题:计算题
分析:利用一个直角梯形的面积分别减去两个直角三角形的面积可得到△AOB面积.
解答: 解:如图,△AOB面积=
解:如图,△AOB面积=
(1+4)×6-
×2×4-
×4×1
=15-4-2
=9.
故答案为9.
 解:如图,△AOB面积=
解:如图,△AOB面积=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=15-4-2
=9.
故答案为9.
点评:本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系.也考查了三角形面积公式.会利用面积的和差计算不规则图形的面积.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
若∠A=34°,则∠A的余角的度数为( )
| A、146° | B、54° |
| C、56° | D、66° |
 如图中的△A′B′C′是由△ABC绕点P旋转180°后得到的图形,根据旋转的性质回答下列问题:
如图中的△A′B′C′是由△ABC绕点P旋转180°后得到的图形,根据旋转的性质回答下列问题: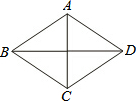 如图,在菱形ABCD中,AC=6,BD=8.
如图,在菱形ABCD中,AC=6,BD=8. 如图所示,CE是BC的延长线.
如图所示,CE是BC的延长线. 数学课上,老师出示了如下框中的题目.
数学课上,老师出示了如下框中的题目. 在正方形ABCD中,O是对角线AC、BD的交点,分别过点A、B、C、D作BD、AC的平行线交于点E、F、G、H.
在正方形ABCD中,O是对角线AC、BD的交点,分别过点A、B、C、D作BD、AC的平行线交于点E、F、G、H.