题目内容
在Rt△ABC中,已知∠C=90°,AC=2BC,现给出下列结论:①sinA=
;②cosB=
;③tanA=2;④sinB=
,则其中结论正确的有( )个.
| ||
| 2 |
2
| ||
| 5 |
| 1 |
| 2 |
| A、3 | B、2 | C、1 | D、0 |
考点:锐角三角函数的定义
专题:
分析:根据勾股定理,可用BC表示AB,根据锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,可得答案.
解答:解:在Rt△ABC中,已知∠C=90°,AC=2BC,
由勾股定理,得
AB=
=
BC.
:①sinA=
=
≠
,故①错误;
②cosB=
=
≠
,故②错误;
③tanA=
=
≠2故③错误;
④sinB=
=
=
≠
,故④错误;
故选:D.
由勾股定理,得
AB=
| AC2+BC2 |
| 5 |
:①sinA=
| BC |
| AB |
| ||
| 5 |
| ||
| 2 |
②cosB=
| BC |
| AB |
| ||
| 5 |
2
| ||
| 5 |
③tanA=
| BC |
| AC |
| 1 |
| 2 |
④sinB=
| AC |
| AB |
| 2BC | ||
|
2
| ||
| 5 |
| 1 |
| 2 |
故选:D.
点评:本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
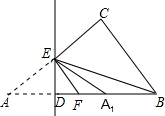 如图,已知Rt△ABC中,AB=5,BC=3,在线段AB上取一点D,作DE⊥AB交AC于E,将△ADE沿DE折叠,设点A落在线段BD上的对应点为A1,又设DA1的中点为F,若△FEA1∽△FBE,则AD等于( )
如图,已知Rt△ABC中,AB=5,BC=3,在线段AB上取一点D,作DE⊥AB交AC于E,将△ADE沿DE折叠,设点A落在线段BD上的对应点为A1,又设DA1的中点为F,若△FEA1∽△FBE,则AD等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
如果有4个不同的整数m、n、p、q满足(2015-m)(2015-n)(2015-p)(2015-q)=4,那么m+n+p+q等于( )
| A、8064 | B、8060 |
| C、8056 | D、8052 |
若∠A=34°,则∠A的余角的度数为( )
| A、146° | B、54° |
| C、56° | D、66° |
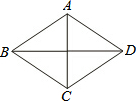 如图,在菱形ABCD中,AC=6,BD=8.
如图,在菱形ABCD中,AC=6,BD=8. 在正方形ABCD中,O是对角线AC、BD的交点,分别过点A、B、C、D作BD、AC的平行线交于点E、F、G、H.
在正方形ABCD中,O是对角线AC、BD的交点,分别过点A、B、C、D作BD、AC的平行线交于点E、F、G、H. 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是中线,CF是∠ACB的平分线,图中相等的锐角为一组,则共有
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是中线,CF是∠ACB的平分线,图中相等的锐角为一组,则共有