题目内容
6.发现:(1)若干平面上三点能够确定一个圆,那么这三点所满足的条件是三点不在同一条直线上.
(2)我们判断四个点A,B,C,D(任意其中个三点不共线)是否在同一圆上时,一般地,先作过A,B,C三点的圆,然后判断点D是否在这个圆上,如果在,则这四个点共圆,如果不在,则不存在同时过这四个点的圆.
思考:
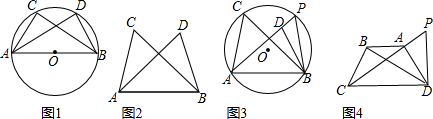
(1)如图1,∠ACB=∠ADB=90°,那么点A,B,C,D四点在(填“在”或“不在”)同一个圆上;
(2)如图2,如果∠ACB=∠ADB=a(a≠90°),(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?芳芳已经证明了点D不在圆内(如图所示),只要能够证明点D也不再圆外,就可以判断点D一定在圆上了,请你完成证明过程.
芳芳的证明过程:
如图3,过A,B,C三点作圆,圆心为O.假设点D在⊙O内,设AD的延长线交⊙O于点P,连接BP.易得∠APB=∠ACB.又由∠ADB是△BPD的外交,得到∠ADB>∠APB,因此∠ADB>∠ACB,这个结论与条件中的∠ACB=∠ADB矛盾,所以点D不在圆内.
应用:
如图4,在四边形ABCD中,连接AC,BD,∠CAD=∠CBD=90°,点P在CA的延长线上,连接DP.若∠ADP=∠ABD.求证:DP为Rt△ACD的外接圆的切线.
分析 发现:(1)根据不在同一条直线上的三点能够确定一个圆即可得到结论;
思考:(1)根据∠ACB=∠ADB=90°,即可得到结论;
(2)如图①,假设点D在⊙O外,设AD交⊙O于点E,连接BE,根据圆周角定理得到∠AEB=∠ACB,根据外角的性质得到∠AEB>∠D于是得到这个结论与条件中的∠ACB=ADB矛盾,即可得到结论;
应用:由∠CAD=∠CBD=90°,推出A,B,C,D四点在以CD为直径的同一个圆上,根据圆周角定理得到∠ACD=∠ABD,推出∠ACD=∠ADP,由于∠ACD+∠ADC=90°,等量代换得到∠ADC+∠ADP=90°,即可得到结论.
解答  解:发现:(1)若平面上三点能够确定一个圆,那么这三点所满足的条件是三点不在同一条直线上,
解:发现:(1)若平面上三点能够确定一个圆,那么这三点所满足的条件是三点不在同一条直线上,
故答案为:三点不在同一条直线上;
思考:(1)∠ACB=∠ADB=90°,那么点A,B,C,D四点在同一个圆上,
故答案为:在;
(2)如图①,假设点D在⊙O外,设AD交⊙O于点E,连接BE,易得∠AEB=∠ACB,又由∠AEB是△BED的外角,∴∠AEB>∠D,∵∠ACB=∠AEB,∴∠ACB>∠ADB,这个结论与条件中的∠ACB=∠ADB矛盾,∴点D不在圆外,
∴D一定在圆上;
应用:∵∠CAD=∠CBD=90°,
∴A,B,C,D四点在以CD为直径的同一个圆上,
∴∠ACD=∠ABD,
∵∠ABD=∠ADP,
∴∠ACD=∠ADP,
∵∠ACD+∠ADC=90°,
∴∠ADC+∠ADP=90°,
∴∠ADP=90°,
∴DP为Rt△ACD的外接圆的切线.
点评 本题考查的是点与圆的位置关系、圆周角定理以及反证法的应用,掌握反证法的一般步骤、同弧所对的圆周角相等是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
13.若a与b互为相反数,m为正整数,则下列两式计算结果互为相反数的是( )
| A. | am与bm | B. | a2m与b2m | C. | am与-bm | D. | a2m与-b2m |
14.小华想找一个解是2的方程,那么他会选择( )
| A. | 3x+6=0 | B. | $\frac{2}{3}$x=2 | C. | 5-3x=1 | D. | 3(x-1)=x+1 |
1.PM2.5指标被纳入今年2月29日国务院批准发布的《环境空气质量标准》.根据该标准,PM2.5一级标准限值为日平均0.000035克/立方米,这一数据用科学记数法表示为( )克/立方米.
| A. | 3.5×10-5 | B. | 3.5×10-4 | C. | 0.35×10-4 | D. | 3.5×10-6 |
16.在下列长度的四根木棒中,能与5cm,11cm长的两根木棒首尾相接,钉成一个三角形的是( )
| A. | 5cm | B. | 6cm | C. | 11cm | D. | 16cm |
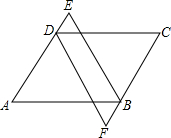 如图,已知AB=CD,AD=BC,DE=BF,说明BE=DF.
如图,已知AB=CD,AD=BC,DE=BF,说明BE=DF.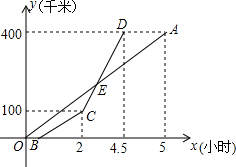 甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题: