题目内容
11.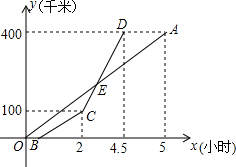 甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发20分钟,且到达乙地后在原地等待货车,在两车相遇后当货车和轿车相距30千米时,求货车所用时间.
分析 (1)设线段CD对应的函数解析式为y=kx+b,由待定系数法求出其解即可;
(2)根据两图象相交的交点指的是两车相遇解答即可.
(3)先由货车和轿车相距30千米列出方程解答即可.
解答 解:(1)设线段CD对应的函数解析式为y=kx+b,
可得:$\left\{\begin{array}{l}{100=2k+b}\\{400=4.5k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=120}\\{b=-140}\end{array}\right.$.
所以线段CD对应的函数表达式为:y=120x-140(2≤x≤4.5);
(2)由图象可得:直线OA的解析式为:y=80x,
根据两图象相交的交点指的是两车相遇,
可得:80x=120x-140,
解得:x=3.5,
把x=3.5代入y=80x,得:y=280;
所以E点的坐标为(3.5,280),即表示当货车出发3.5小时时货车和轿车相遇;
(3)设货车出发xh后,
可得:120x-140-30=80x,
解得:x=4.25.
故答案为:4.25.
(3)由题意知,B($\frac{1}{3}$,0),
∴BC段解析式为y=60x-20($\frac{1}{3}$≤x≤2),
货车与轿车相距30km有四种情况:
1)当$\frac{1}{3}$≤x≤2时,80x-(60x-20)=30,解得x=$\frac{1}{2}$;
2)当2<x≤3.5时,80x-(120x-140)=30,解得x=$\frac{11}{4}$;
3)当3.5<x≤4.5时,120x-140-80x=30,解得x=$\frac{17}{4}$;
4)当4.5<x≤5时,400-80x=30,解得x=$\frac{37}{8}$;
∴x=$\frac{1}{2},\frac{11}{4},\frac{17}{4},\frac{37}{8}$.
点评 本题考查了一次函数的应用,对一次函数图象的意义的理解,待定系数法求一次函数的解析式的运用,行程问题中路程=速度×时间的运用,本题有一定难度,其中求出货车与轿车的速度是解题的关键.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案| A. | (3,-1.5) | B. | (-3,-1.5) | C. | (-2,-3) | D. | (2,-3) |
| A. | 2 | B. | 4 | C. | -2或2 | D. | -4或4 |
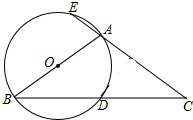 如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,若AC=3AE,则tan∠ABC=$\frac{\sqrt{2}}{2}$.
如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,若AC=3AE,则tan∠ABC=$\frac{\sqrt{2}}{2}$.
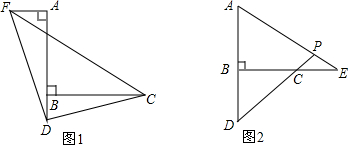
 已知:如图,点A、D、B、E在同一直线上,AC=EF,AD=BE,BC=DF.求证:∠ABC=∠EDF.
已知:如图,点A、D、B、E在同一直线上,AC=EF,AD=BE,BC=DF.求证:∠ABC=∠EDF.