题目内容
13.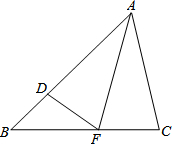 如图,在△ABC中,AB>AC,AF是∠BAC的平分线,D是AB上一点,AD=AC.
如图,在△ABC中,AB>AC,AF是∠BAC的平分线,D是AB上一点,AD=AC.(1)△ADF与△ACF全等吗?为什么?
(2)又过D作DE∥BC交AC于点E,连接CD,请你补全图形,并说明CD是否会平分∠FDE?
分析 (1)AF是∠BAC的平分线,AD=AC,AD为公共边,根据角平分线的性质,利用SAS定理证明△ADF≌△ACF;
(2)由于△ADF≌△ACF利用全等三角形的性质,得DF=CF,则∠FDC=∠DCF,因为DE∥BC,利用平行线的性质,∠EDC=∠DCF,所以∠FDC=∠EDC,即CD平分∠FDE.
解答  (1)解:△ADF≌△ACF,
(1)解:△ADF≌△ACF,
∵AF是∠BAC的平分线,
∴∠DAF=∠FAC,
在△ADF与△ACF中,$\left\{\begin{array}{l}{AD=AC}\\{∠DAF=∠FAC}\\{AF=AF}\end{array}\right.$,
∴△ADF≌△ACF(SAS);
(2)CD平分∠FDE.
∵△ADF≌△ACF,
∴DF=FC,
∴∠FDC=∠FCD,
∵DE∥BC,
∴∠EDC=∠CDF,
∴∠FDC=∠EDC,
∴CD平分∠FDE.
点评 本题主要考查了全等三角形的判定和性质,平行线性质,注意三角形间的公共边是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
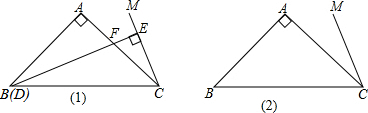
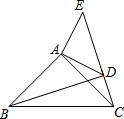 如图,△ACB和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连结BD,则∠BDE=90度.
如图,△ACB和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连结BD,则∠BDE=90度.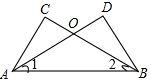 已知如图,在△ABC和△ABD中,AD和BC交于点O,∠1=∠2,请你添加一个条件∠C=∠D(不再添加其它线段,不再标注或使用其它字母),使AC=BD.
已知如图,在△ABC和△ABD中,AD和BC交于点O,∠1=∠2,请你添加一个条件∠C=∠D(不再添加其它线段,不再标注或使用其它字母),使AC=BD. 如图,△ABC中,AB=AC,D为BC边的中点,过C作CE∥AD,交△ABC外角∠MAC的平分线于点E.
如图,△ABC中,AB=AC,D为BC边的中点,过C作CE∥AD,交△ABC外角∠MAC的平分线于点E.