题目内容
3. 如图,△ABC中,AB=AC,D为BC边的中点,过C作CE∥AD,交△ABC外角∠MAC的平分线于点E.
如图,△ABC中,AB=AC,D为BC边的中点,过C作CE∥AD,交△ABC外角∠MAC的平分线于点E.(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形.
分析 (1)首先利用外角性质得出∠B=∠ACB=∠FAE=∠EAC,进而得到AE∥CD,即可求出四边形AEDB是平行四边形,再利用有一个角是直角的平行四边形是矩形即可判定四边形ADCE是矩形;
(2)能使得矩形的临边AD和DC相等的条件均可.
解答 解:(1)∵AB=AC,D为BC中点,
∴AD⊥BC,即∠ADC=90°,∠BAD=∠CAD=$\frac{1}{2}$∠BAC,
∵AE平分∠MAC,
∴∠MAE=∠CAE=$\frac{1}{2}$∠MAC,
又∵∠BAC+∠MAC=180°,
∴∠CAD+∠CAE=$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠MAC=90°,
即∠EAD=90°,
∴∠ADC+∠EAD=180°,
∴AE∥DC,
∵四边形ADCE中,AE∥DC,CE∥AD,
∴四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴四边形ADCE是矩形;
(2)答案不唯一,如当∠BAC=90°时,四边形ADCE是正方形;
点评 本题的考点:外角的性质,等腰三角形的性质(等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.【三线合一】),平行四边形和矩形的判定和性质.

练习册系列答案
相关题目
12. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠BCD=35°,则∠ABD的度数为( )
如图,若AB是⊙O的直径,CD是⊙O的弦,∠BCD=35°,则∠ABD的度数为( )
 如图,若AB是⊙O的直径,CD是⊙O的弦,∠BCD=35°,则∠ABD的度数为( )
如图,若AB是⊙O的直径,CD是⊙O的弦,∠BCD=35°,则∠ABD的度数为( )| A. | 65° | B. | 35° | C. | 55° | D. | 60° |
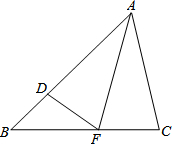 如图,在△ABC中,AB>AC,AF是∠BAC的平分线,D是AB上一点,AD=AC.
如图,在△ABC中,AB>AC,AF是∠BAC的平分线,D是AB上一点,AD=AC. 如图所示,A、B两个旅游点从2011年至2015年“清明小长假”期间的旅游人数变化情况分别用实线和虚线表示,请解答以下问题:
如图所示,A、B两个旅游点从2011年至2015年“清明小长假”期间的旅游人数变化情况分别用实线和虚线表示,请解答以下问题: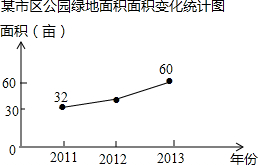 市区某公园的总面积为180亩,它的绿化给公园周边的环境带来了明显的改善,如图是该公园绿地面积的变化统计图,其中2013年绿地面积的增长率是2012年增长率的两倍.
市区某公园的总面积为180亩,它的绿化给公园周边的环境带来了明显的改善,如图是该公园绿地面积的变化统计图,其中2013年绿地面积的增长率是2012年增长率的两倍.