题目内容
11.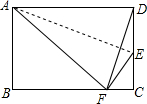 如图,点E为矩形ABCD的边CD上一点,将矩形ABCD沿AE折叠的一边,使点D落在BC边的点F处.若折痕$AE=5\sqrt{10},tan∠EFC=\frac{4}{3}$,则DF的长为3$\sqrt{10}$.
如图,点E为矩形ABCD的边CD上一点,将矩形ABCD沿AE折叠的一边,使点D落在BC边的点F处.若折痕$AE=5\sqrt{10},tan∠EFC=\frac{4}{3}$,则DF的长为3$\sqrt{10}$.
分析 设CE=4k,则CF=3k,由矩形的性质和勾股定理得出EF=5k,∠BAF+∠AFB=90°,由折叠的性质得:∠AFE=∠ADC=90°,DE=EF=5k,AD=AF,AB=CD=9k,证出∠BAF=∠EFC,由三角函数得出BF=12k,由勾股定理得出AD=AF=15k,在Rt△ADE中,由勾股定理得出方程,解方程求出k=1,得出CD=9,CF=3,再由勾股定理求出DF即可.
解答 解:∵tan∠EFC=$\frac{CE}{CF}$=$\frac{4}{3}$,
设CE=4k,则CF=3k,
∵四边形ABCD是矩形,
∴AB=DC,∠ADC=∠B=∠C=90°,
∴EF=$\sqrt{C{E}^{2}+C{F}^{2}}$=5k,∠BAF+∠AFB=90°,
由折叠的性质得:∠AFE=∠ADC=90°,DE=EF=5k,AD=AF,
∴AB=CD=9k,∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
∴tan∠BAF=$\frac{BF}{AB}$=$\frac{4}{3}$,
∴BF=12k,
∴AD=AF=$\sqrt{A{B}^{2}+B{F}^{2}}$=15k,
在Rt△ADE中,AD2+DE2=AE2,AE=5$\sqrt{10}$,
∴(15k)2+(5k)2=(5$\sqrt{10}$)2,
解得:k=1,
∴CD=9,CF=3,
∴DF=$\sqrt{C{F}^{2}+C{D}^{2}}$=$\sqrt{{3}^{2}+{9}^{2}}$=3$\sqrt{10}$;
故答案为:3$\sqrt{10}$.
点评 本题考查了矩形的性质、翻折变换的性质、勾股定理、三角函数的运用;熟练掌握矩形的性质和翻折变换的性质,由勾股定理得出方程是解决问题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
19.点N(a,-b)关于y轴的对称点是坐标是( )
| A. | (-a,b) | B. | (-a,-b) | C. | (a,b) | D. | (-b,a) |
16.下列标志既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
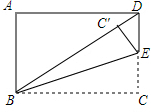 如图,矩形ABCD中,AB=3,BC=5.E为CD边上一点,将矩形沿直线BE折叠,使点C落在BD边上C′处.则DE的长$\frac{34-5\sqrt{34}}{3}$.
如图,矩形ABCD中,AB=3,BC=5.E为CD边上一点,将矩形沿直线BE折叠,使点C落在BD边上C′处.则DE的长$\frac{34-5\sqrt{34}}{3}$.