题目内容
3.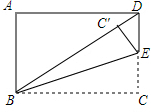 如图,矩形ABCD中,AB=3,BC=5.E为CD边上一点,将矩形沿直线BE折叠,使点C落在BD边上C′处.则DE的长$\frac{34-5\sqrt{34}}{3}$.
如图,矩形ABCD中,AB=3,BC=5.E为CD边上一点,将矩形沿直线BE折叠,使点C落在BD边上C′处.则DE的长$\frac{34-5\sqrt{34}}{3}$.
分析 先利用勾股定理求出线段BD,设DE=x,则EC=EC′=3-x,在RT△EDC′中,由DE2=EC′2+DC′2列出方程即可解决.
解答 解:∵ 四边形ABCD是矩形,
四边形ABCD是矩形,
∴AB=CD=3,BC=AD=5,
∴BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$,
∵△BEC′是由△BEC翻折,
∴BC=BC′=5,EC=EC′,设DE=x,则EC=EC′=3-x,
在RT△EDC′中,∵DE2=EC′2+DC′2,
∴($\sqrt{34}$-5)2+(3-x)2=x2,
∴x=$\frac{34-5\sqrt{34}}{3}$.
故答案为$\frac{34-5\sqrt{34}}{3}$.
点评 本题考查翻折变换、矩形的性质、勾股定理等知识.解题的关键是利用翻折不变性,学会转化的思想,把问题转化为方程解决,是由中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.不等式组$\left\{\begin{array}{l}x-3>2\\ x<3\end{array}\right.$的解集是( )
| A. | x<3 | B. | 3<x<5 | C. | x>5 | D. | 无解 |
 如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,则线段AC的长=9.
如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,则线段AC的长=9.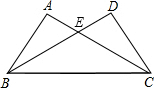 如图,AC与BD交于点E,AB=DC,∠ABC=∠DCB.若∠DBC=35°,求∠ACB的度数.
如图,AC与BD交于点E,AB=DC,∠ABC=∠DCB.若∠DBC=35°,求∠ACB的度数.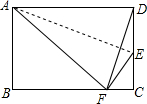 如图,点E为矩形ABCD的边CD上一点,将矩形ABCD沿AE折叠的一边,使点D落在BC边的点F处.若折痕$AE=5\sqrt{10},tan∠EFC=\frac{4}{3}$,则DF的长为3$\sqrt{10}$.
如图,点E为矩形ABCD的边CD上一点,将矩形ABCD沿AE折叠的一边,使点D落在BC边的点F处.若折痕$AE=5\sqrt{10},tan∠EFC=\frac{4}{3}$,则DF的长为3$\sqrt{10}$.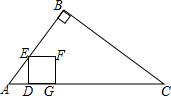 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点D从点A出发以1cm/s的速度运动到点C停止.作DE⊥AC交边AB或BC于点E,以DE为边向右作正方形DEFG.设点D的运动时间为t(s).
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点D从点A出发以1cm/s的速度运动到点C停止.作DE⊥AC交边AB或BC于点E,以DE为边向右作正方形DEFG.设点D的运动时间为t(s).