题目内容
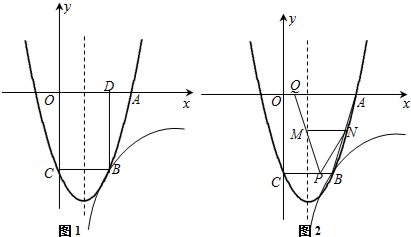
20.如图1,二次函数y=ax2+bx-3的图象与y轴交于点C,与x轴交于点A(3,0),过点C作BC∥x轴,交抛物线于点B,并过点B 作BD⊥x轴,垂足为D.抛物线y=ax2+bx-3和反比例函数$y=\frac{k}{x}$(x>0)的图象都经过点B(2,m),四边形OCBD的面积是6.(1)求反比例函数、二次函数的解析式及抛物线的对称轴;
(2)如图2,点P从B点出发以每秒0.1个单位的速度沿线段BC向C点运动,点Q从O点出发以相同的速度沿线段OA向A点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为t秒.
①当t为何值时,四边形ABPQ为等腰梯形;
②设PQ与对称轴的交点为M,过M点作x轴的平行线交AB于点N,设四边形ANPQ的面积为S,求面积S关于时间t的函数解析式,并指出t的取值范围;当t为何值时,S有最大值或最小值.
分析 (1)根据反比例函数的比例系数k的几何意义可求出k,从而可求出点B的坐标,然后运用待定系数法就可求出二次函数的解析式,由此可求出对称轴方程;
(2)①过点P作PE⊥OA,垂足为E,如图2,易证BC∥OA,要使四边形ABPQ为等腰梯形,只需PQ=AB,只需QE=AD=1,由此即可求出t的值;②如图2,易证△MFP≌△MGQ,则有MF=MG,从而可求出S△BPN(用t表示),然后只需求出S四边形ABPQ,并运用割补法就可得到S关于t的函数解析式,然后只需利用该函数的增减性就可解决问题.
解答 解:(1)如图1,
∵四边形OCBD的面积是6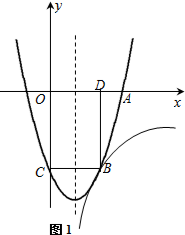 ,
,
∴k=xy=-6,
∴反比例函数的解析式为$y=-\frac{6}{x}$.
∵反比例函数$y=-\frac{6}{x}$(x>0)的图象经过点B(2,m),
∴2m=-6,
解得m=-3.
∴B(2,-3).
将点A(3,0),B(2,-3)代入y=ax2+bx-3,得
$\left\{\begin{array}{l}0=9a+3b-3\\-3=4a+2b-3.\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$,
∴二次函数的解析式y=x2-2x-3.
则抛物线的对称轴为x=-$\frac{-2}{2×1}$=1;
(2)①由题意可知:BP=OQ=0.1t.
∵点B,点C的纵坐标相等,
∴BC∥OA.
过点P作PE⊥OA,垂足为E,如图2.
要使四边形ABPQ为等腰梯形,只需PQ=AB.
即QE=AD=1.
又QE=OE-OQ=(2-0.1t)-0.1t=2-0.2t,
∴2-0.2t=1.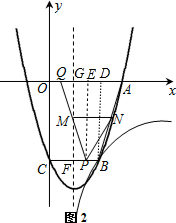
解得t=5,
∴当t=5秒时,四边形ABPQ为等腰梯形.
②设对称轴与BC、x轴的交点分别为F、G,如图2.
∵对称轴x=1是线段BC的垂直平分线,
∴BF=CF=OG=1.
又∵BP=OQ,
∴PF=QG.
∵BC∥OA,
∴∠GQM=∠FPM.
在△MFP和△MGQ中,
$\left\{\begin{array}{l}{∠PMF=∠QMG}\\{∠FPM=∠GQM}\\{PF=QG}\end{array}\right.$
∴△MFP≌△MGQ,
∴MF=MG,
∴S△BPN=$\frac{1}{2}$PB•MF═$\frac{1}{2}$PB•$\frac{1}{2}$FG
=$\frac{1}{2}$×0.1t×$\frac{3}{2}$
=$\frac{3}{40}$t.
∵S四边形ABPQ=$\frac{1}{2}$(BP+AQ)•FG
=$\frac{1}{2}$(0.1t+3-0.1t)•3
=$\frac{9}{2}$,
∴S=S四边形ABPQ-S△BPN
=$\frac{9}{2}$-$\frac{3}{40}$t.
∵BC=2,OA=3,
∴点P运动到点C时停止运动,需要2÷0.1=20秒,
∴0≤t≤20.
∵-$\frac{3}{40}$<0,
∴当t=20秒时,面积S有最小值3.
点评 本题主要考查了运用待定系数法求二次函数的解析式、一次函数的增减性、反比例函数的比例系数k的几何意义、反比例函数图象上点的坐标特征、全等三角形的判定与性质、等腰梯形的判定等知识,把四边形ABPQ为等腰梯形转化为QE=AD是解决第(2)①小题的关键,运用割补法是解决第(2)②小题的关键.

 如图是一个正方体的表面展开图,则原正方体中与“和”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“和”字所在的面相对的面上标的字是( )| A. | 谐 | B. | 强 | C. | 富 | D. | 主 |
| A. | 三角形按边可分为不等边三角形,等腰三角形和等边三角形 | |
| B. | 等腰三角形任一个内角都有可能是钝角或直角 | |
| C. | 三角形的一个外角大于任何一个内角 | |
| D. | 三角形三条内角平分线相交于一点,这点到三角形三边的距离相等 |
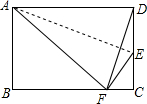 如图,点E为矩形ABCD的边CD上一点,将矩形ABCD沿AE折叠的一边,使点D落在BC边的点F处.若折痕$AE=5\sqrt{10},tan∠EFC=\frac{4}{3}$,则DF的长为3$\sqrt{10}$.
如图,点E为矩形ABCD的边CD上一点,将矩形ABCD沿AE折叠的一边,使点D落在BC边的点F处.若折痕$AE=5\sqrt{10},tan∠EFC=\frac{4}{3}$,则DF的长为3$\sqrt{10}$.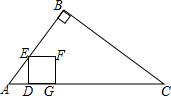 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点D从点A出发以1cm/s的速度运动到点C停止.作DE⊥AC交边AB或BC于点E,以DE为边向右作正方形DEFG.设点D的运动时间为t(s).
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点D从点A出发以1cm/s的速度运动到点C停止.作DE⊥AC交边AB或BC于点E,以DE为边向右作正方形DEFG.设点D的运动时间为t(s).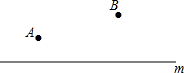 如图,某地由于居民增多,要在公路m上增加一个公共汽车站,A,B是路边两个新建小区,这个公共汽车站建在什么位置,能使两个小区到车站的路程一样长?(保留作图痕迹,不写作法)
如图,某地由于居民增多,要在公路m上增加一个公共汽车站,A,B是路边两个新建小区,这个公共汽车站建在什么位置,能使两个小区到车站的路程一样长?(保留作图痕迹,不写作法)