题目内容
2. 如图,一次函数的图象与直线y=$\frac{3}{2}$x平行,且与直线y=x-2在x轴上相交,则此图象与直线y=x-2及y轴所围成的图形的面积是( )
如图,一次函数的图象与直线y=$\frac{3}{2}$x平行,且与直线y=x-2在x轴上相交,则此图象与直线y=x-2及y轴所围成的图形的面积是( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 41 |
分析 首先根据一次函数的图象与直线y=$\frac{3}{2}$x平行,设一次函数的解析式为y=$\frac{3}{2}$x+b;然后求出直线y=x-2与x轴的交点是(2,0),再把x=2,y=0代入y=$\frac{3}{2}$x+b,求出b的值是多少,判断出一次函数的图象与y轴的交点是多少;最后用一次函数的图象与x轴、y轴围成的图形的面积减去直线y=x-2与x轴、y轴围成的图形的面积,求出此图象与直线y=x-2及y轴所围成的图形的面积是多少即可.
解答 解:∵一次函数的图象与直线y=$\frac{3}{2}$x平行,
∴设一次函数的解析式为y=$\frac{3}{2}$x+b;
直线y=x-2与x轴的交点是(2,0),与y轴的交点是(0,-2),
把x=2,y=0代入y=$\frac{3}{2}$x+b,
可得0=$\frac{3}{2}×2+b$,
解得b=-3,
所以y=$\frac{3}{2}$x+b与y轴的交点是(0,-3),
所以此图象与直线y=x-2及y轴所围成的图形的面积是:
2×|-3|÷2-2×|-2|÷2
=2×3÷2-2×2÷2
=3-2
=1
故选:A.
点评 此题主要考查了两条直线相交、平行问题,解答此题的关键是要明确:直线y=kx+b,(k≠0,且k,b为常数),当k相同,且b不相等,图象平行;当k不同,且b相等,图象相交;当k,b都相同时,两条线段重合,并能求出一次函数的解析式是多少.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
13.-10的绝对值是( )
| A. | $\frac{1}{10}$ | B. | -$\frac{1}{10}$ | C. | 10 | D. | -10 |
17.若关于x的不等式(2-m)x≤m-2的解集为x≥-1,则m应满足的条件是( )
| A. | m>0 | B. | m<2 | C. | m≥2 | D. | m>2 |
11.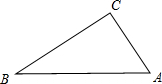 如图,在△ABC中,AB>BC>AC,小华依下列方法作图,①作∠C的角平分线交AB于点D;②作CD的中垂线,分别交AC,BC于点E,F;③连接DE,DF.根据小华所作的图,下列说法中一定正确的是( )
如图,在△ABC中,AB>BC>AC,小华依下列方法作图,①作∠C的角平分线交AB于点D;②作CD的中垂线,分别交AC,BC于点E,F;③连接DE,DF.根据小华所作的图,下列说法中一定正确的是( )
 如图,在△ABC中,AB>BC>AC,小华依下列方法作图,①作∠C的角平分线交AB于点D;②作CD的中垂线,分别交AC,BC于点E,F;③连接DE,DF.根据小华所作的图,下列说法中一定正确的是( )
如图,在△ABC中,AB>BC>AC,小华依下列方法作图,①作∠C的角平分线交AB于点D;②作CD的中垂线,分别交AC,BC于点E,F;③连接DE,DF.根据小华所作的图,下列说法中一定正确的是( )| A. | 四边形CEDF为菱形 | B. | DE=DA | ||
| C. | DF⊥CB | D. | CD=BD |
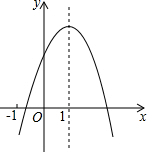 已知二次函数y=ax2+bx+c的图象如图所示,下列结论中,正确的结论的个数( )
已知二次函数y=ax2+bx+c的图象如图所示,下列结论中,正确的结论的个数( )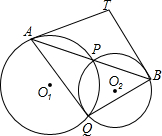 如图,⊙O1与⊙O2相交于P、Q两点,过P点作两圆的割线分别交于⊙O1与⊙O2于A、B,过A、B分别作两圆的切线相交于T,求证:T、A、Q、B四点共圆.
如图,⊙O1与⊙O2相交于P、Q两点,过P点作两圆的割线分别交于⊙O1与⊙O2于A、B,过A、B分别作两圆的切线相交于T,求证:T、A、Q、B四点共圆.