题目内容
12.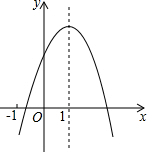 已知二次函数y=ax2+bx+c的图象如图所示,下列结论中,正确的结论的个数( )
已知二次函数y=ax2+bx+c的图象如图所示,下列结论中,正确的结论的个数( )①a+b+c>0;②a-b+c<0;③abc<0;④b=2a; ⑤b>0.
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
分析 根据图象的开口可确定a.再结合对称轴,可确定b,根据图象与y轴的交点位置,可确定c,进行一一分析,即可解答.
解答 解:当x=1时,y=a+b+c,顶点坐标(1,a+b+c),
由图象可知,顶点坐标在第一象限,
∴a+b+c>0,故①正确;
当x=-1时,y=a-b+c,
由图象可知,当x=-1时,所对应的点在第四象限,
∴y=a-b+c<0,故②正确;
∵图象开口向下,
∴a<0,
∵x=-$\frac{b}{2a}$=1,
∴b=-2a,故④错误;
∴b>0,故⑤正确;
∵图象与y轴的交点在y轴的上半轴,
∴c>0,
∴abc<0,故③正确;
∴正确的有4个.
故选:B.
点评 本题考查了二次函数的图象和系数的关系,解题的关键是熟练掌握二次函数的有关性质、以及二次函数的图象的特点.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
3.已知点M(-2,4)在双曲线y=$\frac{m+4}{x}$上,则下列各点一定在该双曲线上的是( )
| A. | (-2,-4) | B. | (4,-2) | C. | (2,4) | D. | (4,2) |
20.在平面直角坐标系中,一次函数y=-3x-2的图象所经过的象限是( )
| A. | 二、三、四 | B. | 一、三、四 | C. | 一、二、四 | D. | 一、二、三 |
2. 如图,一次函数的图象与直线y=$\frac{3}{2}$x平行,且与直线y=x-2在x轴上相交,则此图象与直线y=x-2及y轴所围成的图形的面积是( )
如图,一次函数的图象与直线y=$\frac{3}{2}$x平行,且与直线y=x-2在x轴上相交,则此图象与直线y=x-2及y轴所围成的图形的面积是( )
 如图,一次函数的图象与直线y=$\frac{3}{2}$x平行,且与直线y=x-2在x轴上相交,则此图象与直线y=x-2及y轴所围成的图形的面积是( )
如图,一次函数的图象与直线y=$\frac{3}{2}$x平行,且与直线y=x-2在x轴上相交,则此图象与直线y=x-2及y轴所围成的图形的面积是( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 41 |
 (1)如图所示,在平面直角坐标系中,描出下列3个点,A(-1,0),B(5,0),C(3,4);
(1)如图所示,在平面直角坐标系中,描出下列3个点,A(-1,0),B(5,0),C(3,4);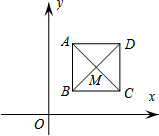 如图,已知正方形ABCD,顶点A(1,3),B(1,1),C(3,1),对角线交于点M.规定“把正方形ABCD先沿x轴翻折,再向左平移个单位”为一次变换,那么经过两次变换后,点M的坐标变为(0,2),连续经过2015次变换后,点M的坐标变为(-2013,-2).
如图,已知正方形ABCD,顶点A(1,3),B(1,1),C(3,1),对角线交于点M.规定“把正方形ABCD先沿x轴翻折,再向左平移个单位”为一次变换,那么经过两次变换后,点M的坐标变为(0,2),连续经过2015次变换后,点M的坐标变为(-2013,-2).