题目内容
17.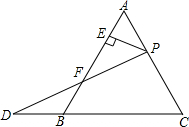 已知等边三角形ABC的边长为12,点P为AC上一点,点D在CB的延长线上,且BD=AP,连接PD交AB于点E,PE⊥AB于点F,则线段EF的长为( )
已知等边三角形ABC的边长为12,点P为AC上一点,点D在CB的延长线上,且BD=AP,连接PD交AB于点E,PE⊥AB于点F,则线段EF的长为( )| A. | 6 | B. | 5 | C. | 4.5 | D. | 与AP的长度有关 |
分析 作DQ⊥AB,交直线AB的延长线于点Q,连接DE,PQ,根据全等三角形的判定定理得出△APE≌△BQF,再由AE=BQ,PE=QD且PE∥QD,可知四边形PEDQ是平行四边形,进而可得出EF=$\frac{1}{2}$AB,由等边△ABC的边长为12可得出DE=6.
解答 解;作DF⊥AB,交AB的延长线于点F,连接DE,PF,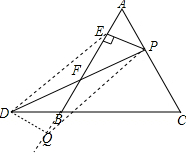
又∵PE⊥AB于E,
∴∠FQD=∠AEP=90°,
∴AP=BD,
∵△ABC是等边三角形,
∴∠A=∠ABC=∠DBQ=60°,
在△APE和△BQD中,
∵∠AEP=∠DBQ=90°,∴∠APE=∠BDQ,
∴在△APE和△BQD中,$\left\{\begin{array}{l}{∠AEP=∠DQB}\\{∠A=∠BDQ}\\{AP=BD}\end{array}\right.$,
∴△APE≌△BQD(AAS),
∴AE=BQ,PE=QD且PE∥QD,
∴四边形PEDQ是平行四边形,
∴EF=$\frac{1}{2}$EQ,
∵EB+AE=BE+BQ=AB,
∴EF=$\frac{1}{2}$AB,
又∵等边△ABC的边长为12,
∴EF=6.
点评 本题考查的是等边三角形的性质及全等三角形的判定定理、平行四边形的判定与性质,根据题意作出辅助线构造出全等三角形是解答此题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
7.2的平方根为( )
| A. | 4 | B. | ±4 | C. | $\sqrt{2}$ | D. | ±$\sqrt{2}$ |
8.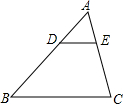 如图,在△ABC中,DE∥BC,若AD=1,DB=2,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,DE∥BC,若AD=1,DB=2,则$\frac{DE}{BC}$的值为( )
 如图,在△ABC中,DE∥BC,若AD=1,DB=2,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,DE∥BC,若AD=1,DB=2,则$\frac{DE}{BC}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
5.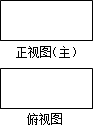 如图,某立体的正视图和俯视图是长、宽分别相等的矩形,给定下列三个命题:
如图,某立体的正视图和俯视图是长、宽分别相等的矩形,给定下列三个命题:
①存在圆柱,其正视图和俯视图如图所示;
②存在正三棱柱,其正视图和俯视图如图所示;
③存在正四棱柱,其正视图和俯视图如图所示;
其中真命题的个数是( )
 如图,某立体的正视图和俯视图是长、宽分别相等的矩形,给定下列三个命题:
如图,某立体的正视图和俯视图是长、宽分别相等的矩形,给定下列三个命题:①存在圆柱,其正视图和俯视图如图所示;
②存在正三棱柱,其正视图和俯视图如图所示;
③存在正四棱柱,其正视图和俯视图如图所示;
其中真命题的个数是( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
12.点P(-2,4)关于坐标原点对称的点的坐标为( )
| A. | (4,-2) | B. | (-4,2) | C. | (2,4) | D. | (2,-4) |
 如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF.
如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF. 如图,直线AB∥CD,直线EF分别交AB、CD于点E、F,若∠AEF=50°,则∠EFC的度数是130°.
如图,直线AB∥CD,直线EF分别交AB、CD于点E、F,若∠AEF=50°,则∠EFC的度数是130°.