题目内容
9. 如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF.
如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF.(1)判断四边形AECF是什么特殊四边形,并证明;
(2)若EF=4,DE=BF=2,求四边形AECF的周长.
分析 (1)连接AC,交BD于点O.利用正方形的性质得出AC⊥BD,OA=OC=OB=OD,进一步得出OE=OF,证得四边形AECF是菱形;
(2)利用菱形的性质和勾股定理求得即可.
解答 解:(1)四边形AECF是菱形,理由如下:
连接AC,交BD于点O,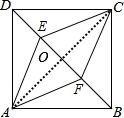
∵四边形ABCD是正方形,
∴AC⊥BD,OA=OC=OB=OD
∴DE=BF
∴OE=OF
∴四边形AECF是菱形;
(2)∵EF=4,DE=BF=2,
∴AC=BD=8,
∴AE=$\sqrt{O{A}^{2}+O{E}^{2}\\;}=\sqrt{{4}^{2}+{2}^{2}}=2\sqrt{5}$,
∴四边形AECF的周长为8$\sqrt{5}$.
点评 此题考查正方形的性质,菱形的判定,勾股定理等知识点,注意结合已知条件合理作出辅助线解决问题.

练习册系列答案
相关题目
20.如果∠α=β,则∠α的补角比其余角大多少度?( )
| A. | 90° | B. | 60° | C. | 180° | D. | 45° |
17.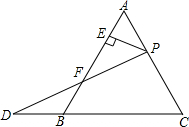 已知等边三角形ABC的边长为12,点P为AC上一点,点D在CB的延长线上,且BD=AP,连接PD交AB于点E,PE⊥AB于点F,则线段EF的长为( )
已知等边三角形ABC的边长为12,点P为AC上一点,点D在CB的延长线上,且BD=AP,连接PD交AB于点E,PE⊥AB于点F,则线段EF的长为( )
 已知等边三角形ABC的边长为12,点P为AC上一点,点D在CB的延长线上,且BD=AP,连接PD交AB于点E,PE⊥AB于点F,则线段EF的长为( )
已知等边三角形ABC的边长为12,点P为AC上一点,点D在CB的延长线上,且BD=AP,连接PD交AB于点E,PE⊥AB于点F,则线段EF的长为( )| A. | 6 | B. | 5 | C. | 4.5 | D. | 与AP的长度有关 |
1.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{xy=1}\\{x+y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+3y=2}\\{y+3z=14}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x-2z=0}\\{x+y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{5x-2y=2}\\{x+y=4}\end{array}\right.$ |