如图.反比例函数y=$\frac{2}{x}$的图象经过矩形OABC的边AB的中点D.则矩形OABC的面积为4．题目和参考答案——青夏教育精英家教网—

题目内容

20．

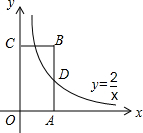如图，反比例函数y=$\frac{2}{x}$的图象经过矩形OABC的边AB的中点D，则矩形OABC的面积为4．

分析可设D点坐标为（x，y），则可表示出B点坐标，从而可表示出矩形OABC的面积，利用xy=2可求得答案．

解答解：
设D（x，y），
∵反比例函数y=$\frac{2}{x}$的图象经过点D，
∴xy=2，
∵D为AB的中点，
∴B（x，2y），
∴OA=x，OC=2y，
∴S_矩形OABC=OA•OC=x•2y=2xy=2×2=4，
故答案为：4．

点评本题主要考查反比例函数k的几何意义，利用条件用D点坐标表示出B点坐标是解题的关键．

练习册系列答案

相关题目

10．已知圆锥的侧面积为15π，底面半径为3，则圆锥的高为（　　）

11．

如图，点P是⊙O外一点，过点P作⊙O的切线PA，切点为A，连接PO，延长PO交⊙O于点B，若∠P=30°，PA=3$\sqrt{3}$，则弧AB的长为2π．

8．观察下列各式：
$\frac{2}{1×3}$=$\frac{1}{1}$-$\frac{1}{3}$；
$\frac{2}{2×4}$=$\frac{1}{2}$-$\frac{1}{4}$；
$\frac{2}{3×5}$=$\frac{1}{3}$-$\frac{1}{5}$；
…
请利用你所得结论，化简代数式：$\frac{1}{1×3}$+$\frac{1}{2×4}$+$\frac{1}{3×5}$+…+$\frac{1}{n（n+2）}$（n≥3且n为整数），其结果为$\frac{3{n}^{2}+5n}{4（n+1）（n+2）}$．

15．已知函数y=ax²-2ax-1（a是常数，a≠0），下列结论正确的是（　　）

	A．	当a=1时，函数图象经过点（-1，1）
	B．	当a=-2时，函数图象与x轴没有交点
	C．	若a＜0，函数图象的顶点始终在x轴的下方
	D．	若a＞0，则当x≥1时，y随x的增大而增大

5．在数1，0，-1，-2中，最大的数是（　　）

12．计算：（-2017）⁰-（$\frac{1}{3}$）^-1+$\sqrt{9}$．

7．要使（x²+ax+1）（x-2）的结果中不含x²项，则a为（　　）

8．

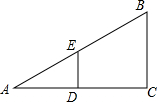如图，在Rt△ABC中，∠ACB=90°，AC=8，AB=10，DE垂直平分AC，交AB于点E，交AC于点D，则DE的长为（　　）

试题分类