题目内容
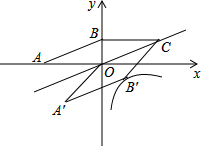 如图,在平面直角坐标系中,平行四边形OABC的顶点A、B的坐标分别为(-10,0)和(0,5).将平行四边形OABC沿边OC所在直线翻折,得到平行四边形OA′B′C,若反比例函数y=
如图,在平面直角坐标系中,平行四边形OABC的顶点A、B的坐标分别为(-10,0)和(0,5).将平行四边形OABC沿边OC所在直线翻折,得到平行四边形OA′B′C,若反比例函数y=| k |
| x |
考点:反比例函数综合题
专题:综合题
分析:连结BB′交OC于E点,根据平行四边形的性质得BC=OA=10,BC∥x轴,则C点坐标为(10,5),则可利用待定系数法确定直线OC的解析式为y=
x,再根据折叠的性质得BE=B′E,CB′CB=10;设B′点坐标为(a,b),则线段BB′的中点E点坐标为(
,
),把E(
,
)代入y=
x得到a=2b+10,由于CB′=10,根据两点间的距离公式得到(a-10)2+(b-5)2=102,则(2b+10-10)2+(b-5)2=102,然后解方程可确定b=-3,则a=4,所以B′点的坐标为(4,-3),再利用反比例函数图象上点的坐标特征得到k=-12.
| 1 |
| 2 |
| a |
| 2 |
| 5+b |
| 2 |
| a |
| 2 |
| 5+b |
| 2 |
| 1 |
| 2 |
解答: 解:连结BB′交OC于E点,如图,
解:连结BB′交OC于E点,如图,
∵四边形ABCO为平行四边形,
∴BC=OA=10,BC∥x轴,
而B(0,5),
∴C点坐标为(10,5),
设直线OC的解析式为y=kx,
把C(10,5)代入得10k=5,解得k=
,
∴直线OC的解析式为y=
x,
∵平行四边形OABC沿边OC所在直线翻折,得到平行四边形OA′B′C,
∴BE=B′E,CB′CB=10,
设B′点坐标为(a,b),则E点坐标为(
,
),
把E(
,
)代入y=
x得
•
=
,
∴a=2b+10,
∵CB′=10,
∴(a-10)2+(b-5)2=102,
∴(2b+10-10)2+(b-5)2=102,
整理得b2-2b-15=0,解得b1=5,b2=-3,
∵B′点在第四象限,
∴b=-3,
∴a=2×(-3)+10=4,
∴B′点的坐标为(4,-3),
∴k=4×(-3)=-12.
故答案为-12.
 解:连结BB′交OC于E点,如图,
解:连结BB′交OC于E点,如图,∵四边形ABCO为平行四边形,
∴BC=OA=10,BC∥x轴,
而B(0,5),
∴C点坐标为(10,5),
设直线OC的解析式为y=kx,
把C(10,5)代入得10k=5,解得k=
| 1 |
| 2 |
∴直线OC的解析式为y=
| 1 |
| 2 |
∵平行四边形OABC沿边OC所在直线翻折,得到平行四边形OA′B′C,
∴BE=B′E,CB′CB=10,
设B′点坐标为(a,b),则E点坐标为(
| a |
| 2 |
| 5+b |
| 2 |
把E(
| a |
| 2 |
| 5+b |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| 5+b |
| 2 |
∴a=2b+10,
∵CB′=10,
∴(a-10)2+(b-5)2=102,
∴(2b+10-10)2+(b-5)2=102,
整理得b2-2b-15=0,解得b1=5,b2=-3,
∵B′点在第四象限,
∴b=-3,
∴a=2×(-3)+10=4,
∴B′点的坐标为(4,-3),
∴k=4×(-3)=-12.
故答案为-12.
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、折叠的性质和平行四边形的性质;会利用待定系数法确定函数解析式和两点的距离公式计算坐标系中两点的线段长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列计算正确的是( )
| A、(a-b)2=a2-b2 |
| B、a2+a2=2a2 |
| C、(a3)2=a5 |
| D、a2•a2=2a2 |
 如图,双曲线
如图,双曲线 如图,点A为x轴负半轴上一点,点B为x轴正半轴上一点,OA,OB(OA<OB)的长分别是关于x的一元二次方程x2-4mx+m2+2=0的两根,C(0,3),且S△ABC=6,则∠ABC的度数为
如图,点A为x轴负半轴上一点,点B为x轴正半轴上一点,OA,OB(OA<OB)的长分别是关于x的一元二次方程x2-4mx+m2+2=0的两根,C(0,3),且S△ABC=6,则∠ABC的度数为