题目内容
将二次函数y=x2-2x-3沿y轴方向向上平移 个单位后和x轴只有一个交点.
考点:二次函数图象与几何变换,抛物线与x轴的交点
专题:
分析:假设将二次函数y=x2-2x-3沿y轴方向向上平移k个单位后和x轴只有一个交点,则方程x2-2x-3+k=0的判别式△=0,由此求出k的值.
解答:解:设将二次函数y=x2-2x-3沿y轴方向向上平移k个单位后和x轴只有一个交点,则平移后的解析式为y=x2-2x-3+k,
由题意,得方程x2-2x-3+k=0的判别式△=0,
所以4-4(-3+k)=0,
解得k=4.
故答案为4.
由题意,得方程x2-2x-3+k=0的判别式△=0,
所以4-4(-3+k)=0,
解得k=4.
故答案为4.
点评:此题主要考查了二次函数图象与几何变换,二次函数图象与x轴交点个数的判定方法,可以与一元二次方程的判别式相结合.

练习册系列答案
相关题目
 如图所示,已知CE∥BD,∠C=∠D,证明:∠A=∠F.
如图所示,已知CE∥BD,∠C=∠D,证明:∠A=∠F. 哈市对教师试卷讲评课中学生参与的深度与广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如下的统计图,请根据图中所给信息解答下列问题:
哈市对教师试卷讲评课中学生参与的深度与广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如下的统计图,请根据图中所给信息解答下列问题: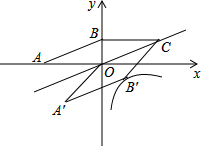 如图,在平面直角坐标系中,平行四边形OABC的顶点A、B的坐标分别为(-10,0)和(0,5).将平行四边形OABC沿边OC所在直线翻折,得到平行四边形OA′B′C,若反比例函数
如图,在平面直角坐标系中,平行四边形OABC的顶点A、B的坐标分别为(-10,0)和(0,5).将平行四边形OABC沿边OC所在直线翻折,得到平行四边形OA′B′C,若反比例函数 以O为端点画六条射线OA,OB,OC,OD,OE,O F,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…,那么所描的第2013个点在射线( )上.
以O为端点画六条射线OA,OB,OC,OD,OE,O F,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…,那么所描的第2013个点在射线( )上.