题目内容
 如图,双曲线y=
如图,双曲线y=| 3 |
| x |
考点:反比例函数综合题
专题:综合题
分析:作AE⊥x轴于E,BC的延长线交x轴于F,易得四边形AEFB为矩形,设C点坐标为(a,
),由于点A的纵坐标是点C的纵坐标的2倍,则B点坐标为(a,
),再利用反比例函数图象上点的坐标特征得到A点坐标为(
,
),然后计算出S△ABC=
,再根据折叠的性质得CB=CB′,∠AB′C=∠B=90°,S△ACB′=S△AB′C=
,而OC平分OA与x轴正半轴的夹角,易正得△OCB′≌△OCF,所以S△OCB′=S△OCF=
×3,于是可得到四边形OABC的面积=3.
| 3 |
| a |
| 6 |
| a |
| a |
| 2 |
| 6 |
| a |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
解答: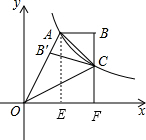 解:作AE⊥x轴于E,BC的延长线交x轴于F,如图,
解:作AE⊥x轴于E,BC的延长线交x轴于F,如图,
∵∠ABC=90°,AB∥x轴,
∴四边形AEFB为矩形,
设C点坐标为(a,
),
∵点A的纵坐标是点C的纵坐标的2倍,
∴AE=2CF,
∴B点坐标为(a,
),
把y=
代入y=
得x=
,
∴A点坐标为(
,
),
∴S△ABC=
(a-
)•
=
,
∵△ABC沿AC翻折后得到△AB′C,
∴CB=CB′,∠AB′C=∠B=90°,S△ACB′=S△AB′C=
而OC平分OA与x轴正半轴的夹角,
∴△OCB′≌△OCF,
∴S△OCB′=S△OCF=
×3,
∴四边形OABC的面积=
+
+
=3.
故答案为3.
 解:作AE⊥x轴于E,BC的延长线交x轴于F,如图,
解:作AE⊥x轴于E,BC的延长线交x轴于F,如图,∵∠ABC=90°,AB∥x轴,
∴四边形AEFB为矩形,
设C点坐标为(a,
| 3 |
| a |
∵点A的纵坐标是点C的纵坐标的2倍,
∴AE=2CF,
∴B点坐标为(a,
| 6 |
| a |
把y=
| 6 |
| a |
| 3 |
| x |
| a |
| 2 |
∴A点坐标为(
| a |
| 2 |
| 6 |
| a |
∴S△ABC=
| 1 |
| 2 |
| a |
| 2 |
| 3 |
| a |
| 3 |
| 4 |
∵△ABC沿AC翻折后得到△AB′C,
∴CB=CB′,∠AB′C=∠B=90°,S△ACB′=S△AB′C=
| 3 |
| 4 |
而OC平分OA与x轴正半轴的夹角,
∴△OCB′≌△OCF,
∴S△OCB′=S△OCF=
| 1 |
| 2 |
∴四边形OABC的面积=
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
故答案为3.
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、反比例函数的比例系数的几何意义和折叠的性质;会利用坐标表示线段和计算三角形面积.

练习册系列答案
相关题目
奇奇开车从北京去少林寺旅游,在高速公路和非高速公路上的行驶速度分别是120千米/时,60千米/时.若奇奇驶完全程用了6小时,其中在高速公路上行驶的路程是在非高速公路上行驶的路程的6倍,则全程长 千米.
在下列四个图案中既是轴对称图形,又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
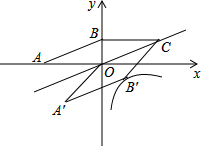 如图,在平面直角坐标系中,平行四边形OABC的顶点A、B的坐标分别为(-10,0)和(0,5).将平行四边形OABC沿边OC所在直线翻折,得到平行四边形OA′B′C,若反比例函数
如图,在平面直角坐标系中,平行四边形OABC的顶点A、B的坐标分别为(-10,0)和(0,5).将平行四边形OABC沿边OC所在直线翻折,得到平行四边形OA′B′C,若反比例函数