题目内容
16. 如图,一堤坝的坡角∠ABC=60°,坡面长度AB=24米(图为横截面).为了使堤坝更加牢固,需要改变堤坝的坡面,为使得坡面的坡角∠ADB=50°,则应将堤坝底端向外拓宽(BD)多少米?(结果精确到0.1米)
如图,一堤坝的坡角∠ABC=60°,坡面长度AB=24米(图为横截面).为了使堤坝更加牢固,需要改变堤坝的坡面,为使得坡面的坡角∠ADB=50°,则应将堤坝底端向外拓宽(BD)多少米?(结果精确到0.1米)(参考数据:$\sqrt{3}$≈1.73,sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)
分析 过A点作AE⊥CD于E.在Rt△ABE中,根据三角函数可得AE,BE,在Rt△ADE中,根据三角函数可得DE,再根据DB=DE-BE即可求解.
解答  解:过A点作AE⊥CD于E.
解:过A点作AE⊥CD于E.
∵在Rt△ABE中,∠ABE=60°,
∴AE=AB•sin60°=24×$\frac{\sqrt{3}}{2}$=12$\sqrt{3}$≈20.76米,
BE=AB•cos60°=24×$\frac{1}{2}$=12米,
∵在Rt△ADE中,∠ADE=50°,
∴DE=$\frac{AE}{tan50°}$≈17.3米,
∴DB=DE-BE≈5.3米.
答:此时应将坝底向外拓宽大约5.3米.
点评 考查了解直角三角形的应用-坡度坡角问题,解答本题的关键是根据所给的坡角构造直角三角形,利用三角函数的知识求解.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
4.正比例函数y=-2x与反比例函数y=$\frac{k}{x}$的图象相交于A(m,2),B两点.则点B的坐标是( )
| A. | (-2,1) | B. | (1,-2) | C. | (-1,2) | D. | (2,-1) |
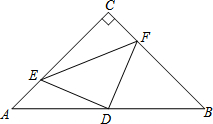 如图,在△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CEDF的周长不变;③点C到线段EF的最大距离为1.其中正确的结论有①③.(填写所有正确结论的序号)
如图,在△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CEDF的周长不变;③点C到线段EF的最大距离为1.其中正确的结论有①③.(填写所有正确结论的序号)