题目内容
15.一次函数y=kx+b与反比例函数$y=\frac{m}{n}$中,若x与y的部分对应值如下表:| x | … | -4 | -2 | -1 | 1 | 2 | 4 | … |
| y=kx+b | … | -1 | 1 | 2 | 4 | 5 | 7 | … |
| $y=\frac{m}{x}$ | … | -1 | -2 | -4 | 4 | 2 | 1 | … |
分析 由表得出直线和双曲线的交点,画出直线和双曲线的大致图象,由$\frac{m}{x}>kx+b$知反比例函数图象在一次函数图象上方,结合图象可得答案.
解答 解:由表可知y=kx+b与$y=\frac{m}{x}$交于点(-4,-1)和点(1,4),
用描点法可得出二者的大致图象.
若$\frac{m}{x}>kx+b$,则反比例函数图象在一次函数图象上方,
由函数图象可知解集为x<-4或0<x<1,
故答案为:x<-4或0<x<1.
点评 本题考查了一次函数和反比例函数的交点问题,给出相应的函数值,求自变量的取值范围应该从交点入手思考.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
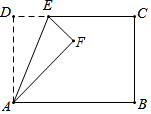 如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为$\frac{5}{2}$或10.
如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为$\frac{5}{2}$或10.